Uvod
U dugogodišnjem radu s učenicima i studentima na svim razinama obrazovanja (od osnovne škole do fakulteta) primijetili smo da im koncepti opsega i površine često nisu u potpunosti jasni, usprkos činjenici da se s njima upoznaju još od 3. razreda osnovne škole. Navedene pojmove teško ili nikako ne povezuju sa svakodnevnim životnim potrebama, a često ih ne uspijevaju objasniti niti svojim riječima. Na pitanje što je opseg ili površina nekog lika, učenici se pokušavaju grozničavo prisjetiti formule jer taj pojam, umjesto s njegovim značenjem, povezuju s određenom formulom. Kako tih formula ima više pa ih se ne mogu točno prisjetiti ili ih miješaju, njihovi odgovori često budu besmisleni ili netočni, a sam pojam ne mogu i ne znaju drukčije objasniti. Ovakav ishod, naravno, ne zadovoljava niti učenike niti nas učitelje, a dugoročno predstavlja problem za njihove životne potrebe jer je riječ o pojmovima koji nam u životu veoma često trebaju. Kako je matematika predmet u kojem su mnogi pojmovi i postupci apstraktni (poput primjerice funkcija, razlike kvadrata ili sustava jednadžbi), ovakvi konkretni pojmovi koje bi lako mogli povezati s realnošću prava su dragocjenost koju bismo trebali iskoristiti za motiviranje učenika i njihovo približavanje matematici. Problem postaje još ozbiljniji kada uočimo da i studenti odgojno obrazovnih usmjerenja (odgojitelji predškolske djece, učitelji razredne nastave, pedagozi, pa i poneki studenti matematike i prirodnih znanosti) ne uspijevaju ove pojmove odrediti i definirati na primjeren način. Suvremena nastava matematike naglašava važnost konceptualnog razumijevanja matematike kao i važnost njezine primjene u problemskim i životnim situacijama (Mišurac, 2014.).
Opseg i površina
Kod koncepata opsega i površine riječ je o mjerljivim svojstvima konkretnih objekata (ravninskih likova), koji se uče i razvijaju na način da učenici odmah mogu vidjeti njihovu svrhu, značenje i primjenu kroz primjenu u realističnim problemima. Kurikulum matematike posebno naglašava važnost domene mjerenja, a među ishodima iz ove domene izdvajaju se: usvajanje standardnih mjernih jedinica, mjerenje odgovarajućim mjernim uređajima, procjenjivanje, preračunavanje i izračunavanje određenih veličina. Očekuje se prepoznavanje mjerivih obilježja geometrijskih oblika i pojava uz razložnu i učinkovitu upotrebu alata i tehnologije, a očekuje se i da se rezultati interpretiraju i izražavaju u jedinici mjere koja odgovara situaciji. Ističe se zahtjev da učenici povežu matematiku s drugim odgojno-obrazovnim područjima, s vlastitim iskustvom, svakodnevnim životom u kući i zajednici te na radnome mjestu, prepoznaju mjeriva obilježja ravninskih i prostornih oblika u umjetnosti te ih upotrebljavaju za opis i analizu svijeta oko sebe. Uz to, matematički procesi naglašavaju važnost povezivanja različitih dijelova matematike, povezivanje matematike sa životom, poticanje razvoja komunikacijskih vještina, rješavanje problema i logičko zaključivanje.
Problemski zadatak
Upravo na tom tragu nastala je ideja za problemski zadatak ,,Gradimo uz pomoć matematike” koji smo proveli prvo u nastavi matematike u 8. razredu, a zatim tijekom dvije godine (2022. i 2023.) s učenicima 8. razreda u okviru Centra izvrsnosti
Splitsko-dalmatinske županije u sekciji Matematika. U zadatku su učenici proučavali jedan konkretan, njima razumljiv i blizak životni problem iz područja građevinarstva (ali i ekonomije), u kojem su ove pojmove morali upotrebljavati u njihovom punom značenju te ih povezivati s određenim dijelovima zadatka. Problem koji je postavljen pred učenike bio je odabir terena i gradnja jednostavne stambene kuće što veće površine unutar određenog zadanog budžeta od 350 000 eura. U troškove građenja ubrajamo kupnju zemljišta, izgradnju vanjskih zidova kuće, njezinog poda i krova, a sam teren potrebno je ograditi ogradom. Kuća može biti prizemnica ili jednokatnica, a moguće su i varijacije, primjerice da se nad prizemljem izgradi kat ili samo dio gornjeg kata. Pritom su morali poštovati određene standarde građenja, poput činjenice da je maksimalna izgrađenost zemljišta 30 % njegove ukupne površine, da zid kuće mora biti udaljen minimalno 3 metra od ruba terena i 5 metara od prometnice. Uz kuću je trebalo osigurati i šest parkirališnih mjesta minimalne dimenzije 2.5 m$\times$5 m, a na terenu je trebalo i planirati vrt koji je pravokutnog oblika i zauzima minimalno 20 % površine terena. Od troškova građenja morali su računati na cijenu zidanja i uređenja zida u iznosu od 200 €/m$^{2}$ i poda u iznosu od 100 €/m$^{2}$, a cijena dužnog metra ograde za teren iznosi 200 €/m. Navedeni podatci uzeti su aproksimativno, ali realistično iz razgovora s arhitektima i građevinarima.
Učenicima je ponuđeno šest terena različitih oblika i različite cijene po m$^{2}$ (slika 1). Oblici parcela sastavljeni su od osnovnih geometrijskih oblika pravokutnika, trapeza i pravokutnih trokuta što olakšava izračun potrebnih površina. Kod prikazivanja terena nisu bile zadane sve duljine stranica, ali one koje nisu bile zadane mogle su se odrediti ili izračunati (najčešće primjenom Pitagorina poučka).
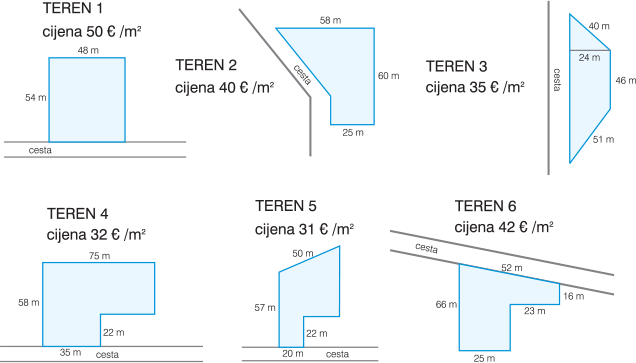
Od učenika se očekivalo da prouče sve ponuđene terene, da procijene (izračunaju) veličinu površine na kojoj se kuća smije nalaziti, da odrede gdje bi je na odabranom terenu smjestili i da odrede oblik svoje kuće kako bi dobili što veću stambenu površinu u okviru zadanog budžeta. Naravno, očekivali smo da u navedenim pokušajima osvijeste da je oblik kvadrata najekonomičniji oblik izgradnje jer se najmanjim opsegom može obuhvatiti najveća moguća površina. Kako je želja da površina kuće bude što veća, ali unutar zadanog budžeta, a cijena direktno ovisi i o opsegu i o površini kuće, jasno je da je kuća kvadratnog oblika optimalnija od one pravokutne. Ipak, ponekad i oblik terena može utjecati na konačan oblik pa sve parametre treba uzeti u obzir. Činjenica da kuća može biti prizemna, ali i da je moguće podići još kat čini zadatak još kompleksnijim.
Problem koji je stavljen pred učenike veoma je zahtjevan i traži poznavanje brojnih matematičkih koncepata poput računanja postotaka, površina, opsega, oplošja, Pitagorina poučka, skiciranja, poznavanja geometrijskih oblika, vizualizaciju i snalaženje na tlocrtu, povezivanje svih navedenih koncepata i povezivanje sa životom. Ipak, sam zadatak je učenicima bio izrazito zanimljiv, izazovan i potaknuo ih je na dublje razumijevanje navedenih pojmova. Učenici su na zadatku radili u manjim grupama (do 4 učenika u skupini) i to tijekom 6 nastavnih satova.
Provedba zadatka
Prije provođenja zadatka s učenicima u Centru izvrsnosti, sličan zadatak, u malo pojednostavljenom obliku, proveli smo s učenicima 8. razreda osnovne škole Marjan u Splitu, njih 37, i to kao samostalni projektni zadatak. (To je napravljeno u proljeće 2021. dok su još bile na snazi epidemiološke mjere i povremena online nastava za vrijeme pandemije Covida-19.) Za proučavanje materijala, osmišljavanje ideja i računanje potrebnih parametara učenici su imali dva tjedna, nakon čega su trebali predstaviti svoje zaključke ostalima. Analiza samog problemskog zadatka provedena je frontalno u razredu kako bismo bili sigurni da su učenici potpuno razumjeli što se od njih traži, a nakon toga su rad nastavili samostalno kod kuće. Problem koji su dobili bio je veoma sličan prethodno opisanom problemu, osim što je bio jednostavniji i kraći. Ponuđena su im tri terena, cijena izgradnje ovisila je samo o zidovima, zanemarujući troškove poda i krovišta. Nisu trebali zadovoljiti uvjet o maksimalno 30 %-tnoj izgrađenosti zemljišta, nije im bio ograničen budžet i nisu morali osigurati mjesta za parkiralište i vrt. Cilj im je bio izgraditi kuću što je moguće veće površine sa što manjim troškovima. Pokazalo se da je otprilike četvrtina učenika (njih 9) jednostavno odabrala teren s najjeftinijom cijenom kvadrata ne sagledavajući ostale aspekte koji utječu na konačnu cijenu. Čak polovina učenika (njih 18) odabralo je proizvoljno jedno zemljište i na njemu smjestilo kuću, ne pokušavajući proučiti/istražiti ostale terene, što pokazuje nedostatak sustavnosti u radu. Malo više od četvrtine učenika (njih 10) uspjelo je u istraživačkom dijelu zadatka doći do zaključka da je oblik kvadrata ekonomičniji za gradnju kuće jer manjim opsegom uspijemo zahvatiti veću površinu objekta. U razgovoru s učenicima saznali smo da im je rad na zadatku bio zanimljiv, da su bili motivirani i zainteresirani za rad na njemu, da su produbili svoje znanje o površini i opsegu i kako bi voljeli da ovakvog rada u nastavi ima više.
Ohrabreni navedenim rezultatima, problem smo proširili ranije opisanim detaljima i tijekom dvije godine proveli ga s učenicima osmih razreda nadarenima za matematiku koji su se uključili u rad u Centru izvrsnosti tijekom tri subote (po dva sata). Očekivali smo da će u startu njihove spoznaje o opsegu i površini biti jasnije nego kod prosječnih učenika, ali pokazalo se da tu nema velikih razlika. I oni su navedenim pojmovima pristupali prvenstveno kroz formule i smatrali su da su opseg i površina lika međusobno povezani (da veći opseg nužno znači i veću površinu).
Kako bi oni osvijestili odnos površine i opsega, osmislili smo dva zadatka (prema NCTM, 2000) koje smo u početku s njima proveli.
ZADATAK 1.
Imate 36 jediničnih kvadrata i od njih slažete različite pravokutne oblike. Svakom obliku koji prikažete izračunajte opseg i površinu. Što primjećujete? Pokušajte generalizirati zaključak.ZADATAK 2.
Imate 36 štapića duljine 1 dm i od njih slažete različite pravokutne oblike. Svakom obliku koji prikažete izračunajte opseg i površinu. Što primjećujete? Pokušajte generalizirati zaključak.
Rješavajući navedene zadatke, učenici su uočili da je kvadratni oblik onaj gdje uz najmanji opseg zahvaćamo najveću površinu i taj im je zaključak bio polazište u pristupu našeg problema građenja uz pomoć matematike. U nastavku rada detaljno smo analizirali problemski zadatak i učenici su ga u skupinama rješavali.
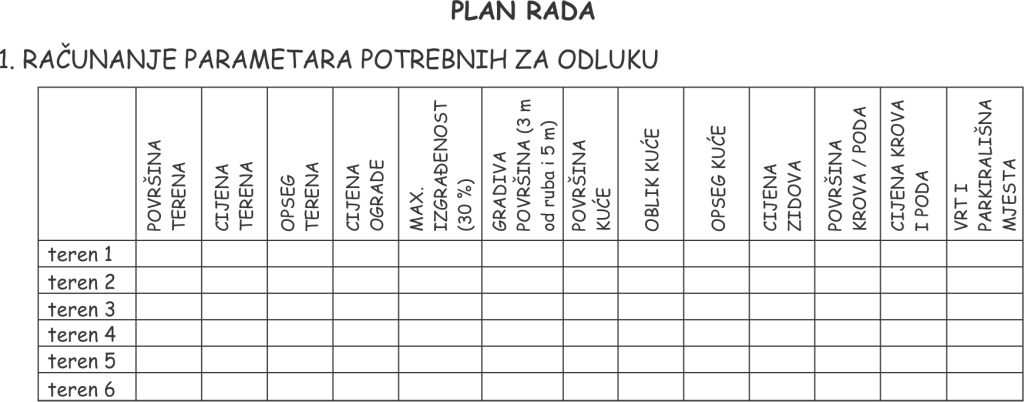
Kako bi odabrali optimalni teren, morali su računati površinu i opseg svakog od njih te određivati koliko bi im novca iz budžeta preostalo nakon kupnje i ograđivanja pojedinog zemljišta. Nakon toga, su uglavnom proračunavali kolika bi maksimalno mogla biti kuća koju na određenu parcelu mogu smjestiti te dozvoljava li im oblik terena i pripadna ograničenja (udaljenost od ruba i od prometnice) građenje kvadratne kuće. Nakon toga, trebalo je izračunati cijenu građenja za svaku odabranu kuću i provjeriti imaju li dostatan iznos za tu izgradnju. Zaključili su da im osiguravanje parkirališnih mjesta i vrta ne utječe bitno na rješenje problema pa su se orijentirali na ostale parametre problema. Zadatak se pokazao izrazito zahtjevan, ima mnogo računanja i mogućih rješenja, a uz to mogućnost izgradnje kata kuće dodatno uvećava broj rješenja. Kako bismo im olakšali praćenje rezultata i osigurali sistematičnost u pristupu zadatku, ponudili smo im i tablicu u koju su mogli upisivati svoje izračune i s pomoću nje uspoređivati različite opcije (slika 2).
Kako se i navedenih 6 sati pokazalo premalo za sve potrebno u ovom projektnom zadatku, učenici bi na kraju uglavnom odabrali jedan od terena (najčešće teren 2) i na njemu smjestili kvadratnu prizemnu kuću. Usprkos velikom radu i zahtjevnom računanju učenici su bili jako zainteresirani, motivirani i zadovoljni radom i onim što su osvijestili. Reakcije su bile veoma pozitivne, a procijenili su da će se spoznajama do kojih su došli koristiti u životu.
Zaključak
Osim ostvarivanja matematičkih ishoda nastavom potičemo i ostvarujemo i ishode međupredmetnih tema. Uz ovaj zadatak posebno bismo istaknuli međupredmetnu temu Poduzetništvo, koja navodi da u nastavi
svih predmeta treba razvijati učenikove poduzetničke kompetencije usvajanjem poduzetničkih znanja, vještina i stavova nužnih za pripremu i sudjelovanje u svijetu rada. Posebna domena u ovoj međupredmetnoj temi je domena ekonomske i financijske pismenost koja predviđa da se učenike putem nastavnih sadržaja uvodi u svijet rada i financija, stjecanje i raspodjelu rezultata. Na taj mu način omogućujemo osnovno razumijevanje ekonomije i poduzetničkoga djelovanja kao procesa stvaranja nove vrijednosti te djelovanja tržišnih zakonitosti. Upravo to potiče se navedenim problemskim zadatkom ,,Gradimo uz pomoć matematike”.
Reakcije učenika bile su izrazito pozitivne, navodili su nam da bi rad na ovakvim životnim problemima bio mnogo korisniji i interesantniji nego tradicionalno učenje te da bi rado sudjelovali u sličnim projektima. Nadamo se da će opisana ideja i zadatak potaknuti i druge učitelje na poučavanje ovih i drugih važnih pojmova rješavajući životne probleme, a da će učenicima biti od velike koristi za njihovo buduće matematičko, ali i svako drugo obrazovanje.
Literatura
- Ministarstvo odgoja i obrazovanja (MZO) (2019.): Kurikulumi nastavnih predmeta Matematika za osnovne škole i gimnazije i Matematika za srednje strukovne škole na razini 4.2.
- Ministarstvo odgoja i obrazovanja (MZO) (2019.): Kurikulum međupredmetne teme Poduzetništvo za osnovne i srednje škole.
- I. Mišurac (2014.): Suvremeni standardi matematičkih kompetencija u početnoj nastavi matematike, Filozofski fakultet Sveučilišta u Splitu, Split. National Council of Teachers of Mathematics (2000.): Principles and standards for school mathematics, Reston, VA: NCTM.
