Zanimljivosti o broju 121

Matematičari pa i oni koji se ne smatraju njima rado promišljaju o svojstvima prirodnih brojeva i uočavaju razne karakteristike koje pojedini broj posjeduje i koje ga povezuju odnosno razlikuju od ostalih. Tako i redni broj časopisa koji je pred vama ima neka zanimljiva svojstva.

Odmah se uočava da je broj $121$ palindromski broj, tj. broj koji se jednako čita s lijeva odnosno s desna. Nastao je kvadriranjem broja $11$, također palindromskog broja. Zanimljivo je da je su i sljedeće dvije potencije broja $11$ također palindromski brojevi:
$${11}^2=121,{11}^3=1331{11}^4=14641.$$
Zapis broja $121$ ostaje palindrom i u nekim drugim bazama: ${121}_{(10)}={171}_{(8)}={11111}_{(3)}$.

Broj $121$ je najmanji troznamenkasti briljantni broj. Briljantni su oni prirodni brojevi koji su umnožak dvaju prostih brojeva s jednakim brojem znamenaka. Tako je $121=11\cdot 11$ i oba faktora $11$ su prosti brojevi jednake duljine (2). Najveći troznamenkasti briljantni broj je $989$ jer je prikaziv kao $23\cdot 43$. Pronađite sve dvoznamenkaste i troznamenkaste briljantne brojeve.

Broj $121$ pripada i skupini Smithovih brojeva. To su brojevi koji se mogu rastaviti na proste faktore tako da je zbroj znamenaka svih faktora jednak zbroju znamenaka samog broja.
$$\begin{array}{rl}& 121=11\cdot 11,\text{zbroj znamenaka broja }121\text{ je}1+2+1=4,\\ & \text{ i zbroj znamenaka faktora }11\text{ i }11\text{ jednak je }(1+1)+(1+1)=4.\end{array}$$
Broj $121$ je najmanji troznamenkasti Smithov broj, dok je $985$ najveći troznamenkasti Smithov broj $(985=5\cdot 197$ i zbrojevi znamenaka su $9+8+5=22$ te $5+(1+9+7)=22)$. Pronađite ostale troznamenkaste Smithove brojeve.

Broj $121$ je petnaesti broj u seriji centralnih poligonalnih brojeva. U engleskom govornom području ovi brojevi imaju i šaljive nazive kao što su: pancake number (engl. pancake: palačinka) ili lazy caterer number (engl. lazy caterer: lijeni ugostitelj).

Centralni poligonalni brojevi povezani su s problemom podjele kruga (ravnine) na najveći broj dijelova s pomoću pravaca. Promotrimo podjele kruga za prvih nekoliko slučajeva.

S brojem $n$ označimo broj pravaca kojima dijelimo krug, a s $f(n)$ broj dijelova na koje je krug podijeljen s $n$ pravaca. Jasno je da će se najveći broj dijelova pojaviti kad se svi pravci u parovima sijeku unutar kruga, ali nikoja tri se ne sijeku u jednoj točki.

Ako je $n=1$, tada je $f(1)=2$. Ako je $n=2$, tada je $f(2)=4$. Ako je $n=3$, tada je $f(3)=7$.

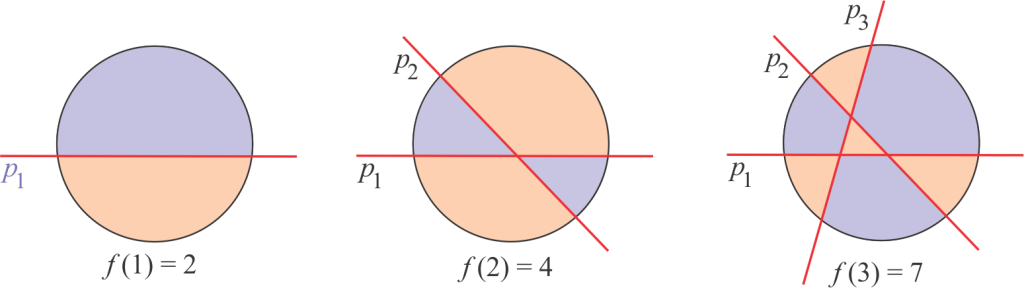
Pogledajmo posljednju sliku, za $n=3$.

Kad povučemo još jedan pravac, on će presjeći postojeća tri pravca čime će se postojeći broj dijelova kruga povećati za 4. Naime, novi pravac prolazi kroz četiri dijela kruga koja su nastala prethodnom podjelom i svaki od ta četiri dijela dijeli na dva nova dijela.

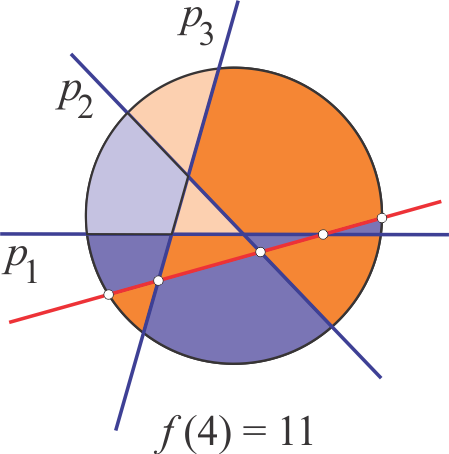
Dakle, $f(4)=4+f(3)=4+7=11$. Ovo se zaključivanje provodi i za opći $n$. Naime, ako imamo krug koji je već podijeljen na $f(n-1)$ dijelova s pomoću $n-1$ pravaca, tada novi, $n$-ti pravac dijeli postojećih $n-1$ dijelova kruga na dva dijela te se ukupni broj dijelova povećava za $n-1$. Stoga rekurzija koja opisuje podjelu kruga glasi ovako:
$$f(n)=f(n-1)+n,n\ge 2,f(1)=2.$$

Rješavanjem ove rekurzije dobivamo:
$$\begin{array}{rl}f(n)& =n+f(n-1)\\ & =n+(n-1)+f(n-2)\\ & =n+(n-1)+\dots +f(2)\\ & =n+(n-1)+\dots +2+f(1)\\ & =n+(n-1)+\dots +2+2\\ & =\frac{n(n+1)}{2}+1.\end{array}$$

Dakle, najveći broj dijelova kruga koje dobivamo povlačenjem pravaca jednak je
$$f(n)=\frac{n(n+1)}{2}+1,\text{ tj. }f(n)=(\genfrac{}{}{0ex}{}{n+1}{2})+1.$$
Broj $121$ se dobiva za $n=15$, tj. kad krug siječemo s 15 pravaca, tada je najveći mogući broj dijelova kruga jednak $121$.

---