Diferencirana nastava matematike ili adaptivno podučavanje?Pitanje je sad – Miš

Ovaj rad uspoređuje dva pristupa u nastavi matematike – diferenciranu nastavu i adaptivno podučavanje. Oba pristupa imaju cilj prilagoditi nastavu različitim potrebama učenika, ali na različite načine. Dok diferencirana nastava unaprijed prilagođava sadržaje, metode i okruženje, adaptivnim podučavanjem učitelj reagira na potrebe učenika u stvarnom vremenu. U radu su dani i konkretni primjeri zadataka koji omogućuju primjenu oba pristupa, čime se osigurava dinamično i inkluzivno obrazovno okruženje.

Ključne riječi: diferencirana nastava, adaptivno podučavanje, tipovi zadataka

Razmislite koliko vam zapravo odgovara odjeća univerzalne veličine (engl. one size). Vjerojatno ne u potpunosti. Slično je i s jedinstvenim pristupom u nastavi. Jedinstveni model ne može zadovoljiti potrebe svih učenika. Svaki učenik ima svoje specifičnosti, od sposobnosti i interesa do načina na koji najbolje uči, stoga je važno prilagoditi nastavu tim različitostima. Jedan od učinkovitih načina prilagodbe je diferencirana nastava. Ovaj pristup omogućuje prilagodbu zadataka prema razinama težine, u skladu s mogućnostima i potrebama učenika. Na taj način svi učenici dobivaju priliku za napredak, bilo da im je potrebna dodatna podrška ili veći izazovi [6]. Ipak, sam pojam diferencijacije često nosi negativne konotacije jer ga mnogi učitelji doživljavaju kao dodatno opterećenje, što može dovesti do iscrpljenosti i nezadovoljstva u ionako zahtjevnom poslu. Osim toga, kruta primjena diferencijacije može izazvati probleme u praksi. Na primjer, učenici koji postižu bolje rezultate u matematici ponekad skrivaju svoje znanje kako bi izbjegli dodatne zadatke, dok učenici s manje uspjeha postaju obeshrabreni jer smatraju da ne mogu držati korak s vršnjacima ili pristupiti složenijim zadatcima. Ovakvi izazovi ističu potrebu za fleksibilnijim i osjetljivijim pristupima u prilagodbi nastave.

Danas se kao alternativa diferencijaciji naširoko promiče ideja adaptivnog podučavanja. Ona se temelji na uvjerenju da učenicima nisu potrebni samo različiti zadatci, već i različite razine podrške i prilagodbe u različitim fazama nastavnog procesa. Iako ideja prilagodbe nije nova, adaptivno podučavanje naglašava ono što je diferencijacija zapravo trebala biti – osjetljivost na individualne potrebe učenika i fleksibilnost u pristupu. No zapravo se čini kao da smo stari izraz zamijenili novim jer je upravo sama bit diferencijacije uvijek bila osigurati svakom učeniku priliku za napredak u skladu s njegovim individualnim mogućnostima i potrebama.

Ipak, postoje određene razlike. Diferencijacija je proaktivna jer se oslanja na sposobnost predviđanja kako će učenici razumjeti matematički sadržaj. Adaptivno podučavanje, s druge strane, jest reaktivno. U adaptivnom podučavanju učitelji prilagođavaju svoj pristup kako bi odgovorili na potrebe učenika u stvarnom vremenu, što ga čini sve popularnijim posljednjih godina, osobito uz primjenu tehnologije [1]. Adaptivno podučavanje događa se kada učitelj tijekom nastave primijeti učenike koji djeluju zbunjeno. Učitelj tada odvaja vrijeme za rad s njima i razjašnjava njihove pogrešne predodžbe, dok ostatak razreda nastavlja raditi na zadanim zadatcima. Ipak, učinkovito podučavanje često integrira elemente oba pristupa, pa bismo mogli reći da je diferencijacija adaptivno podučavanje na makrorazini, dok je prilagodba tijekom nastave adaptivno podučavanje na mikrorazini [5].

Diferencijacija

U ovom dijelu članka objasnit ćemo glavne ideje diferencijacije. Diferencirana nastava stavlja učenika u središte nastavnog procesa, prepoznajući njegove individualne potrebe, interese i sposobnosti. Učitelj nastoji razumjeti učenikove stilove učenja, prethodna znanja i emocionalne potrebe kako bi mu pružio adekvatnu podršku. Diferencirana nastava izrazito je korisna za osmišljavanje nastave u heterogenim razredima [11]. Cilj takve nastave nije zadržati učenika na razini na kojoj se nalazi, već putem osmišljenih aktivnosti potaknuti ga na ostvarivanje bolje razine akademskih postignuća. Diferencirani pristup oslanja se na prilagodbu četiriju elemenata, tj. sadržaja, procesa, proizvoda i okruženja za učenje (Slika 1).

Sadržaj se odnosi na informacije, koncepte i vještine koje učenici trebaju svladati. Diferencirana nastava omogućuje prilagodbu sadržaja kako bi učenici učili na razini usklađenoj s njihovim individualnim potrebama. Ključna ideja je rad na istom sadržaju jer definira osnovu onoga što se uči. Ako je učenje temeljeno na ishodima, učitelj detaljno razrađuje razine tih ishoda. Učenici sa slabijim znanjem mogu rješavati zadatke koji obuhvaćaju ishode na osnovnoj razini, dok napredniji učenici mogu raditi na zadatcima koji uključuju ishode na izvrsnoj razini, povezujući ih s drugim temama ili primjenjujući ih na praktične probleme.

Proces se odnosi na metode i aktivnosti putem kojih učenici uče. Diferenciranje procesa uključuje prilagodbu strategija podučavanja kako bi učenici sudjelovali u nastavi na način koji im najbolje odgovara. Na primjer, učenici mogu raditi samostalno ako im je potreban mir, u paru ili skupinama ako vole razmjenu ideja i suradnju, ili putem interaktivnih aktivnosti poput radionica. Brzina učenja također se može prilagoditi: neki učenici napreduju vlastitim tempom, dok napredniji mogu istraživati dodatne materijale i ići ispred ostalih.

Proizvod označava načine na koje učenici pokazuju stečeno znanje i vještine, odnosno načine na koje se učenici vrednuju. Diferenciranje proizvoda omogućuje učenicima odabir načina na koji će predstaviti naučeno, čime se dodatno potiču njihovi interesi i sposobnosti. Na primjer, neki učenici mogu pisati ispit, drugi kreirati poster, treći videozapis ili prezentaciju. Tehnologija se ovdje može koristiti za izradu digitalnih materijala, poput animacija, blogova ili online projekata. Za učenike s poteškoćama posebno je korisno prilagođeno vrednovanje koja pruža više načina za izražavanja stečenih znanja i vještina.

Okruženje za učenje ostvaruje se prilagodbom učionice kako bi se zadovoljile socijalne i emocionalne potrebe učenika. Ova vrsta diferencijacije može uključivati fizičko prilagođavanje učionice ili omogućavanje učeniku da radi samostalno, umjesto u skupini. Mogu se kreirati različite zone u učionici, poput prostora za rad u skupni, individualni rad i praktične aktivnosti. Može se omogućiti fleksibilan raspored namještaja koji se lako može razmještati. Npr. stolovi u krug za diskusiju ili grupirati klupe za rad u grupama. Važno je i osigurati pristup resursima. To znači osigurati dostupan materijal za različite stilove učenja (vizualne, auditivne, kinestetičke).

Što to znači za nastavu matemtike? Ako se u razrednom odjelu nalaze učenici s različitim razinama znanja, nekoliko je mogućnosti prilagodbe:

Učitelj matematike može prilagoditi sadržaj. Ako su tema operacije s razlomcima, slabiji se učenici mogu koristiti vizualnim prikazima i zbrajati razlomke jednakih nazivnika. Napredni učenici mogu raditi na složenijim problemima, poput primjene razlomaka u svakodnevnim situacijama.
Učitelj matematike može prilagoditi proces. Kada se uči geometrija, neki se učenici mogu koristiti digitalnim alatima za crtanje, dok drugi mogu izrađivati modele od papira ili drugih materijala. Učenici koji bolje uče auditivno mogu sudjelovati u raspravama o osobinama figura.
Učitelj matematike može prilagoditi proizvod. Ako je tema računanje s postotcima, napredni učenici mogu osmisliti i predstaviti financijski plan koji uključuje korištenje postotaka (npr. štednja ili porezi), dok slabiji učenici mogu računati popust na jednostavnim primjerima.

Ove teorijske postavke ukazuju da se diferencijacija u nastavi matematike može ostvariti u svim njezinima fazama: fazi obrade/usvajanje novih sadržaja, fazi konsolidacije (rješavanje zadataka odmah nakon usvajanja), fazi vježbanja i ponavljanja te fazi vrednovanja znanja [9].

Diferencijacija u nastavi matematike

U broju 116 ovog časopisa, autori Mikulić, Filipov i Liščić [7] opisali su diferencijaciju s pomoću projektne nastave matematike. No, ne moraju učitelji uvijek provoditi projektnu nastavu kako bi proveli učinkovitu diferencijaciju. Mi ćemo se u ovom dijelu članka osvrnuti na ideje za fazu uvježbavanja.

Cvjetni zadatci

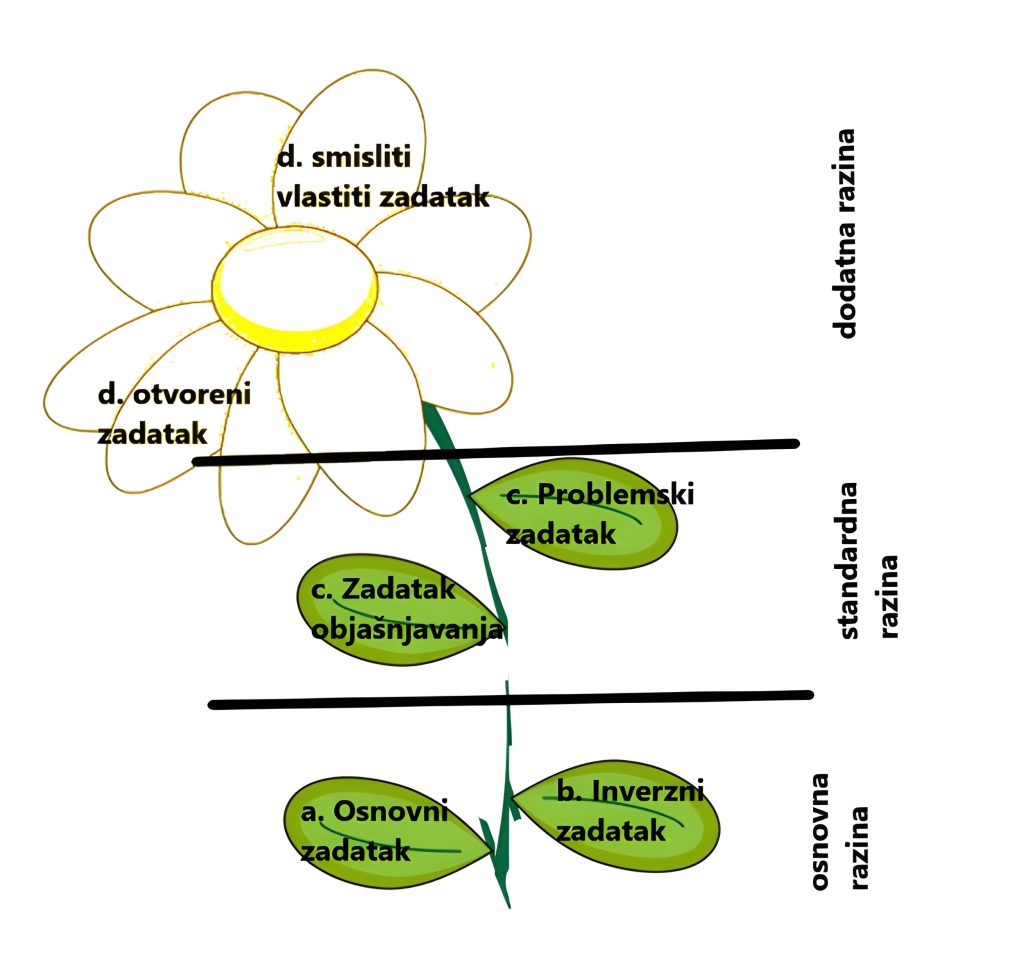
Cvjetni zadatci (njem. Blütenaufgaben) dizajnirani su tako da omogućuju diferencirani pristup učenju matematike. Zadatci imaju središnji zadatak/temu i više opcionalnih dodatnih dijelova (latica), od kojih svaka latica nudi različit izazov (Slika 2). Cvjetni zadatci sastoje se od nekoliko podzadataka s različitom težinom na istu temu. Započinju zatvorenim zadatkom koji je prikladan svim učenicima [4]. Slijede podzadatci u kojima se težina, tj. zahtjevnost i složenost povećavaju korak po korak. Razine cvjetnog zadatka prikazane su na Slici 2. Ovakav tip zadatka omogućuje učenicima rad na razini koja odgovara njihovim sposobnostima i potrebama.

**Slika 2.** Ilustracija cvjetnog zadatka

Kako bismo razjasnili kakvog su oblika podzadatci u cvjetnom zadatku, potrebno je poznavati tipologiju zadataka. Nju smo prikazali u sljedećoj tablici:

tip zadatka	početna situacija	način rješavanja	rješenje	opis
riješeni primjer	+	+	+	Zadana je početna situacija, način rješavanja i rješenje zadatka.
osnovni zadatak	+	+	–	Zadatak je u cijelosti određen i zadan je način rješavanja.
inverzni zadatak	–	+	+	Dan je rezultat i način rješavanja, a učenici trebaju pronaći prikladnu situaciju (tekst zadatka).
zadatak objašnjavanja	+	–	+	Učenici trebaju objasniti je li zadatak točno riješen ili ne.
problemski zadatak	+	–	–	Način rješavanja zadatka nije zadan.
inverzni problemski zadatak	–	–	+	Zadano je rješenje, ali učenici ne znaju ni način rješavanja ni početnu situaciju.
zadatak otvorenog tipa	–	+	–	Poznat je način rješavanja. Učenici sami smišljaju zadatak.
osmisliti vlastiti zadatak (potpuno otvoren zadatak)	–	–	–	U otvorenoj situaciji ništa nije zadano. Učenici trebaju sami osmisliti sve dijelove zadatka i na kraju ga riješiti.

Tablica 1. Tipovi zadataka [2]

Pogledajmo sada primjere cvjetnih zadataka.

Primjer 1. Dijeljenje razlomaka

Izračunaj $\frac{4}{9} \cdot \frac{2}{3}$ .

+ + –

osnovni zadatak

Karlo je izračunao da je $\frac{33}{20}$ rezultat dijeljenja $1 \frac{2}{3} : 2 \frac{3}{4}$ . Je li Karlo u pravu? Objasni.

+ – +

zadatak objašnjavanja

Odredi broj koji dijeljenjem s $\frac{1}{3}$ daje isti rezultat kao kada mu se pribroji $\frac{1}{3}$ .

+ – –

problemski zadatak

Napiši tri različita zadatka dijeljenja s rezultatom $\frac{4}{3}$ .

– – +

inverzni problemski zadatak

Smisli zadatak za dijeljenje razlomaka u kojem se pojavljuje račun $\frac{7}{5} \cdot \frac{2}{9}$ . Riješi zadatak.

– + –

zadatak otvorenog tipa

Primjer 2. Decimalni brojevi

Franka naručuje opremu za svoj novi bicikl. Artikli koje planira naručiti su:

biciklistička kaciga (0.6 kg)
lokot za bicikl (1 kg)
prednje i stražnje svjetlo za bicikl (0.4 kg)
pumpa za bicikl (0.7 kg)
set alata za popravak (0.8 kg)
rezervna unutarnja guma (0.3 kg)
boca za vodu (0.2 kg).

Troškovi dostave su sljedeći:

mali paket do 3 kg – cijena dostave je 3.5 €
srednji paket do 5 kg – cijena dostave je 5 €
veliki paket do 7 kg – cijena dostave je 7.90 €.

(osnovna razina)
a) Koliko će Franka platiti za dostavu ako naruči sve artikle? Objasni.

(standardna razina)
b) Franka želi smanjiti masu narudžbe kako bi iskoristila povoljniju dostavu za srednji ili mali paket. Koje artikle može izostaviti kako bi najbolje iskoristila trošak dostave srednjeg paketa? Objasni.

(dodatna razina)
c) U posebnoj akciji trošak dostave za male pakete do 2 kg iznosi samo 2 €. Koje bi artikle bi Franka mogla naručiti u tom slučaju kako bi iskoristila ovu dodatnu uštedu?

Primjer 3. Algebarski izrazi

Lana daje Martinu zagonetku s brojevima: “Zamisli broj. Dodaj mu 1 i pomnoži rezultat s 5. Na kraju oduzmi 4 od posljednjeg broja. Ako mi kažeš rezultat, reći ću ti broj koji si zamislio!”

(osnovna razina)
a) Martin je zamislio broj 6. Koji je rezultat dobio?
b) Sada Martin smišlja novi broj. Njegov rezultat je 76. Koji je broj zamislio?

(standardna razina)
c) Kako Lana prema rezultatu može izračunati broj koji Martin zamisli?

(dodatna razina)
d) Smislite svoju zagonetku i navedite odgovarajuću strategiju rješavanja.

Cvjetni zadatak ne bi trebao imati više od pet podzadataka [3]. Mora početi osnovnom razinom, ali nije potrebno riješiti sve zadatke. Ukupno vrijeme za rješavanje cvjetnog zadatka treba ograničiti na otprilike 20 minuta.

Paralelno diferencirajući zadatci

Paralelno diferencirajući zadatci predstavljaju vrstu zadataka osmišljenih tako da svi učenici rade na istom sadržaju, ali na različitim razinama složenosti. Ova vrsta zadataka omogućava učenicima rad na zadatcima koji odgovaraju njihovim trenutačnim sposobnostima. Kod paralelno diferencirajućih zadataka možemo se poslužiti sljedećom idejom. Svaki zadatak ima nekoliko razina, pri čemu vrijedi:

1 zvjezdica	* laka razina
2 zvjezdice	** srednja razina
3 zvjezdice	*** izazov

Svaki učenik može birati zadatak prema vlastitim sposobnostima ili uz savjet učitelja. Također učitelj učenicima može podijeliti listić za samovrednovanje kako bi učenici procijenili razinu svojih sposobnosti za ovu temu. Svaki učenik može rješavati zadatke u zadanom vremenu tako da “sakupi” određeni broj zvjezdica, a broj zvjezdica određuje učitelj.

Pogledajmo primjere paralelno diferencirajućih zadataka.

Primjer 4. Kvadratne jednadžbe

Osnovna razina (1 zvjezdica):

Riješi kvadratnu jednadžbu: $x^{2} - 5 x + 6 = 0$ .
Riješi kvadratnu jednadžbu s pomoću faktorizacije: $x^{2} - 9 = 0$ .
Riješi kvadratnu jednadžbu: $x^{2} - 4 x = 0$ .

Srednja razina (2 zvjezdice):

Riješi kvadratnu jednadžbu s pomoću formule za kvadratne jednadžbe: $2 x^{2} - 8 x + 6 = 0$ .
Riješi kvadratnu jednadžbu i odredi prirodu rješenja (jedno ili dva različita realna rješenja): $x^{2} - 6 x + 9 = 0$ .
Riješi kvadratnu jednadžbu koristeći se diskriminantom i zaokruži rješenja na jednu decimalu: $3 x^{2} - 12 x + 9 = 0$ .

Napredna razina (3 zvjezdice):

Riješi jednadžbu $4 x^{2} - 12 x + 9 = 0$ te objasni povezanost rezultata s kvadratom binoma.
Riješi jednadžbu $x^{2} - 4 x + 3 = 0$ primjenjujući više metoda (faktorizacija, formula) te usporedi dobivene rezultate.
Nađi sve realne vrijednosti parametra $k$ za koje kvadratna jednadžba $x^{2} + k x + (k + 1) = 0$ ima dva različita realna korijena.

Primjer 5. Zbrajanje i oduzimanje razlomaka

Odaberi i riješi zadatke tako da prikupiš najmanje 6 zvjezdica.

*1. a) $\frac{1}{3} + \frac{2}{3}$

b) $\frac{2}{7} + \frac{1}{7}$

c) $\frac{3}{8} + \frac{5}{8}$

**2. a) $\frac{1}{4} + \frac{2}{3}$

b) $\frac{1}{3} + \frac{2}{5}$

c) $\frac{2}{3} + \frac{5}{6}$

***3. a) $2 \frac{2}{7} + 1 \frac{3}{7}$

b) $1 \frac{2}{3} + 2 \frac{1}{5}$

c) $3 \frac{5}{8} + 4 \frac{5}{6}$

***4. a) Oduzmi $\frac{1}{2} - \frac{1}{3}$ . Nacrtaj odgovarajuću sliku.

5. Dopiši brojeve koji nedostaju tako da račun bude točan.

*a) $\frac{3}{9} + \frac{2}{}$

*b) $\frac{29}{} + \frac{}{37} = \frac{36}{37}$

*c) $\frac{13}{23} + \frac{}{} = \frac{19}{23}$

**d) $\frac{7}{12} + \frac{1}{6} = \frac{}{}$

**e) $\frac{1}{4} + \frac{}{8} = \frac{1}{2}$

**f) $\frac{}{11} - \frac{1}{2} = \frac{5}{22}$

Korištenje udžbenika

Ako učitelj ne želi kreirati dodatne materijale, može se poslužiti zadatcima iz udžbenika. Udžbenici sadrže zadatke različitih težina koje učitelj može uspješno iskoristiti za ovakav tip nastave. Zadatci se rješavaju uz određene uvjete koje učitelj mora jasno iskomunicirati s učenicima ili ih zapisati na ploču ili ih projicirati. Primjerice, učitelj zadaje zadatke iz udžbenika 1-7. Učenici koji su uspješno riješili Zadatke 1- 3, prelaze na Zadatke 8- 14. Tko griješi u Zadatcima 1-3, nastavlja dalje rješavati Zadatke 4 – 7. Zatim, učenici koji su upješno riješili Zadatke 8 -10, prelaze na Zadatke 15 -16. Oni koji griješe u Zadatcima 8-10, nastavljaju dalje sa Zadatcima 11-14.

Ideja diferencirane nastave nije da svi učenici rješavaju sve zadatake, nego da učitelj slabijim učenicima omogući dodatnu potporu i vježbanje, a naprednijim učenicima omogući pristup izazovnijim zadatcima. Također, diferencijacija neće biti uspješna ako samo učitelj određuje koju razinu učenik treba rješavati. Niti će diferencijacija biti uspješna ako učenici uvijek samostalno biraju razinu na kojoj će raditi. Za uspješnu diferencijaciju potrebna je kombinacija oba pristupa ovisno o situaciji učenja.

Adaptivno podučavanje

Zajednička karakteristika onog što nazivamo diferencirana nastava i adaptivno podučavanje jest briga o učenicima različitih sposobnosti. Cilj diferencirane nastave nije neprekidan rad na nižoj razini, već i uvođenje zadataka viših razina kako bi učenik ostvario svoj potencijal. Također, adaptivno se podučavanje ne može provoditi bez odgovarajuće pripreme. Zapravo se diferencirana nastava i adaptivno podučavanje nadopunjuju, a planiranje diferencijacije može poslužiti kao temelj adaptivnog podučavanja [8]. Pripremajući se unaprijed, učitelji osiguravaju raznovrsne resurse i strategije za učinkovitu podršku svakom učeniku. Takav pristup pojednostavnjuje početnu izvedbu nastave i stvara fleksibilnu strukturu unutar koje se može odvijati adaptivno podučavanje. Kada sat započne, adaptivno podučavanje dolazi do izražaja. Primjenjujući diferencirane aktivnosti, učitelji mogu lakše uočiti kako učenici pristupaju sadržaju i lakše prepoznati gdje učenici imaju poteškoća ili gdje napreduju. Na temelju povratnih informacija u stvarnom vremenu učitelj može prilagođavati svoju nastavu. Na primjer, ako skupina učenika ima problema s razumijevanjem kako zbrajati razlomke, učitelj se može usmjeriti na ponovno objašnjavanje pojma zajedničkog nazivnika, koristeći se vizualnim prikazima ili konkretima pripremljenim tijekom faze planiranja, dok ostali učenici rješavaju zadatke koje je učitelj pripremio za vježbanje.

Zaključak

Kombiniranjem diferenciranja i adaptivnog podučavanja učitelji stvaraju dinamično i inkluzivno okruženje za učenje. Faza planiranja osigurava da su od početka dostupni raznovrsni putevi učenja, dok adaptivno podučavanje omogućava prilagodbe u stvarnom vremenu prema potrebama učenika. Razine kojima učenici pristupaju određuju se dijagnostičkim vrednovanjem na početku sata, kao i kontinuiranim formativnim vrednovanjem tijekom sata. Uočimo da oba pristupa zahtijevaju od učitelja dobro poznavanje svojih učenike, kontinuirano praćenje njihova napretka i balansiranje različitih zahtjeva, što može dovesti do njihova preopterećenja. Ako se nastava u stvarnom vremenu stalno prilagođava, to može stvoriti kaos ili nedosljednost, posebno ako učenici nisu navikli na takav pristup. S druge strane, može se pojaviti percepcija nepravde među učenicima. Neki učenici mogu osjetiti da su favorizirani ili da se prema njima postupa drukčije, što može izazvati frustraciju ili smanjiti motivaciju. No unatoč ovim potencijalno negativnim aspektima, integracija diferenciranja i adaptivnog podučavanja osigurava da svi učenici dobiju potrebnu podršku za uspjeh, čineći proces učenja i učinkovitijim i pravednijim. Naime, istraživanja pokazuju da prilagođavanje potrebama učenika pozitivno utječe na ishode učenja [6, 10].

Literatura

A. Blažić, L. Bulian, R. Ivanković, J. Jović, Lj. Jukić Matić, E. Kantor, A. Krampač-Grljušić, B. Majdiš, Z. Pichler i T. Stipančić (2024.): Development of the adaptive learning concept at CARNET, 15th International Conference on e-Learning, Beograd.
R. Bruder (2003.): Konstruieren – auswählen – begleiten. Über den Umgang mit Aufgaben, u H. Ball (Ur.), Aufgaben. Lernen fördern – Selbstständigkeit entwickeln (str. 12-15). Friedrich Jahresheft.
R. Bruder i J. Reibold (2010.): Weil jeder anders lernt – Ein alltagstaugliches Konzept zur Binnendifferenzierung. Mathematik lehren, 162, str. 2-9.
B. Grave, i R. Thiemann (2010.): Erfahrungen mit Blütenaufgaben Komplexe Aufgaben zugänglich machen, Mathematik lernen 162, str. 18-21
I. Hardy, J. Decristan i E. Klieme (2019.): Adaptive teaching in research on learning and instruction, Journal for educational research online, 11, str. 169-191.
B. N. Langelaan, L. Gaikhorst, W. Smets i R. J. Oostdam (2024.): Differentiating instruction: Understanding the key elements for successful teacher preparation and development, Teaching and Teacher Education, 140, 104464. https://doi.org/10.1016/j.tate.2023.104464
M. Mikulić, M. Filipov i D. Liščić (2022.): Učeničkim projektom do diferencijacije u nastavi matematike, Matematika i škola, 116, str. 3-12.
S. A. Parsons, S. L. Dodman & S. C. Burrowbridge (2013): Broadening the view of differentiated instruction. Phi Delta Kappan, 95, str. 38–42.
S. Prediger i C. Scherres (2012.): Niveauangemessenheit von Arbeitsprozessen in selbstdifferenzierenden Lernumgebungen. Journal Für Mathematik-Dida)ktik, 33, str.143–173. https://doi.org/10.1007/s13138-012-0035-9
S. Steenbergen-Hu, M.C. Makel, P. Olszewski-Kubilius (2016.): What one hundred years of research says about the effects of ability grouping and acceleration on K–12 students’ academic achievement: Findings of two second-order meta-analyses, Review of Educational Research, 86, str. 849-899.
C. A. Tomlinson (2017.): How to differentiate instruction in mixed-ability classrooms. ASCD, Arlington VA.

Brankica Majdiš, učitelj izvrsni savjetnik, OŠ „Mladost“, Osijek Ljerka Jukić Matić, izvanredni profesor, Fakultet primijenjene matematike i informatike, Sveučilište u Osijeku