Ovo je treći i završni članak serije o računanju površine raznostraničnih trokuta. Detaljno se predstavlja sedam mogućih postupaka rješavanja tog problema školske matematike u važnom slučaju kada su duljine stranica trokuta različiti kvadratni korijeni koji su iracionalni brojevi.
U prvom članku [1] opisana je povijest računanja površine trokuta sa stranicama $13$, $14$ i $15$. Pokazano je da su povijesno bila ravnopravno prisutna dva postupka. U prvom se postupku najprije nalazilo da je visina na stranicu $14$ jednaka $12$, da bi se potom primijenila formula po kojoj je površina trokuta ($84$) jednaka polovini umnoška baze ($14$) i visine ($12$). U alternativnom se postupku direktno upotrijebila Heronova formula.
Drugi članak [2] prikazao je evoluciju odnosa tih dvaju postupaka u udžbenicima matematike. U njemu je ukazano i na moguće negativne posljedice po kreativno mišljenje učenika ako se (direktno ili indirektno) promiče pogrešna ideja da je korištenje Heronove formule superioran postupak računanja površine raznostraničnog trokuta kada su zadane duljine svih triju stranica.
Nažalost, eksplicitne i argumentirane kritike te pogrešne ideje rijetko se nalaze u udžbenicima matematike.
Griswold, Keedy i Schacht [3], kao Keedy, Griswold, Schacht i Mamary [4] su, na primjer, za slučaj kada su poznate Kartezijeve koordinate vrhova, napomenuli sljedeće:
,,Možemo se koristiti formulom za udaljenost (točaka) kako bismo odredili duljine stranica i nakon toga upotrijebiti Heronovu formulu da nađemo površinu. Takvo računanje može biti komplicirano ako su dužine iracionalni brojevi.”
Za slučaj trokuta, čije su Kartezijeve koordinate vrhova $(2,3)$, $(5,7)$ i $(6,1)$, predlažu jednostavniju metodu u kojoj se tražena površina dobiva ako se od pridruženog pravokutnika ($4\times 6$) oduzme zbroj površina triju pravokutnih trokuta s katetama $(2,4)$, $(4, 3)$ i $(1,6)$:
$$
P = 24-(4 + 6 + 3) = 24-13 = 11.
$$Ono što nije pokazano jest da su duljine dviju stranica razmatranog trokuta doista iracionalni brojevi. U ovom su slučaju duljine stranica dva iracionalna broja $\sqrt {20}$ i $\sqrt{37}$, te racionalni broj 5.
Također su propustili spomenuti moguću upotrebu formule za računanje površine trokuta kada su poznate Kartezijeve koordinate njegovih vrhova [5, 6, 7].
To nije propustio Aggarwal [8] jer nudi sljedeći komentar:
,,U devetom smo se razredu koristili Heronovom formulom za nalaženje površine trokuta kada su zadane duljine njegovih stranica. Međutim, to može biti mukotrpno, posebno ako su duljine stranica iracionalni brojevi. Pogledajmo postoji li neki lakši način.”
Kao ,,lakši način” Aggarwal izvodi formulu za računanje površine trokuta kada su zadane Kartezijeve koordinate njegovih vrhova.
Kao i u ranijoj kritici, ne dokazuje se da su stranice trokuta u primjerima u kojima se primjenjuje izvedena formula doista iracionalni brojevi. Također se ne spominje mogući alternativni ,,lakši način” kada se tražena površina nalazi oduzimanjem površina triju pravokutnih trokuta od površine pridruženog pravokutnika [3, 4].
Nalaženje površine trokuta s iracionalnim stranicama korištenjem Heronove formule
Kako u predočenim kritikama nije pokazano da je korištenje Heronove formule za nalaženje površine trokuta s iracionalnim stranicama ,,komplicirano” [3, 4] ili ,,mukotrpno” [8], korisno je eksplicitno tražiti od učenika da upoznaju detalje takvog korištenja [9]:
,,Koristeći se Heronovom formulom za površinu trokuta:
$$
P=\sqrt{s(s-a)(s-b)(s-c)},
$$gdje je $s=\dfrac{a+b+c}{2}$, izračunaj površinu trokuta kojemu su zadane duljine stranica: $a=\sqrt{10}$, $b=\sqrt{20}$, $c=\sqrt{26}$.”
Traženi umnožak iz kojeg treba izvaditi kvadratni korijen čine faktori čije su vrijednosti:
$$
\begin{align}
s&=\dfrac{\sqrt{10}+\sqrt{20}+\sqrt{26}}{2}\\
\left(s-a\right)&=\dfrac{\sqrt{20}+\sqrt{26}-\sqrt{10}}{2}\\
\left(s-b\right)&=\dfrac{\sqrt{10}+\sqrt{26}-\sqrt{20}}{2}\\
\left(s-c\right)&=\dfrac{\sqrt{10}+\sqrt{20}-\sqrt{26}}{2}.
\end{align}
$$Taj umnožak je:
$$
\begin{align}
&s\left(s-a\right)\left(s-b\right)\left(s-c\right)=\\
&= \dfrac{\sqrt{10}+\sqrt{20}+\sqrt{26}}{2}\cdot \dfrac{\sqrt{20}+\sqrt{26}-\sqrt{10}}{2}\cdot\dfrac{\sqrt{10}+\sqrt{26}-\sqrt{20}}{2}.\dfrac{\sqrt{10}+\sqrt{20}-\sqrt{26}}{2}\\
&= \dfrac{1}{16}[(\sqrt{200}+\sqrt{260}-10)+(20+\sqrt{520}-\sqrt{200})\\
&\qquad +(\sqrt{520}+26-\sqrt{260})]\cdot[(10+\sqrt{200}-\sqrt{260})\\
&\qquad +(\sqrt{260}+\sqrt{520}-26)-(\sqrt{200}+20-\sqrt{520})]\\
&=\dfrac{1}{16}(2\sqrt{520}+36)(2\sqrt{520}-36) \\
&=\dfrac{1}{16} (2080-1296) = 49.
\end{align}
$$Tražena površina zadanog trokuta s iracionalnim stranicama $\sqrt{10}$, $\sqrt{20}$ i $\sqrt{26}$ jednaka je:
$$
P=\sqrt{49} = 7.
$$Jasno je da je za učenike ovaj postupak kompliciran i mukotrpan jer zahtijeva oprezno izvođenje aritmetičkih operacija kako bi se izbjegle moguće računske pogreške.
Postupak se može djelomično pojednostavniti ako se primijeni alternativni oblik Heronove formule koji navodi Dunham [10]:
$$
P=\dfrac{1}{4}\sqrt{2\left(a^2b^2+a^2c^2+b^2c^2\right)-\left(a^4+b^4+c^4\right)}.
$$Korištenje druge i četvrte potencije stranica značajno skraćuje nalaženje površine ovog trokuta čije su stranice kvadratni korijeni $\sqrt{10}$, $\sqrt{20}$ i $\sqrt{26}$:
$$
\begin{align}
P&=\dfrac{1}{4}\sqrt{2\left(10.20+10.26+20.26\right)-\left(100+400+676\right)}\\
&=\dfrac{1}{4}\sqrt{2\left(200+260+520\right)-1176}\\
&=\dfrac{1}{4}\cdot\sqrt{1960-1176}\\
&=\dfrac{1}{4}\cdot\sqrt{784}=\dfrac{1}{4}\cdot28=7.
\end{align}
$$
U nastavku slijedi izlaganje pet drukčijih postupaka koji omogućuju nalaženja površine ovog trokuta s iracionalnim stranicama. Njihovo predstavljanje učenicima, nakon što su površinu našli primjenom uobičajenog oblika Heronove formule, može pomoći u eliminiranju pogrešnog učeničkog vjerovanja koje često inducira tradicionalna nastava matematike: Za svaki matematički zadatak postoji samo jedan jedini način rješavanja!
Nalaženje površine trokuta s iracionalnim stranicama korištenjem dvaju poznatih postupaka računanja visine
Kako je prikazano u prvom članku [1], površina raznostraničnog trokuta nalazi se tako da se u prvom koraku izračuna duljina visine spuštene na jednu od stranica. U drugom koraku se nađe polovina umnoška visine i te stranice.
Taj algebarski pristup moguće je primijeniti i kada su stranice iracionalni brojevi. U trokutu koji nas zanima visina se spušta na stranicu duljine $\sqrt{26}$, dijeleći je na dva dijela: $x$ i $\sqrt{26}-x$ (slika 1).
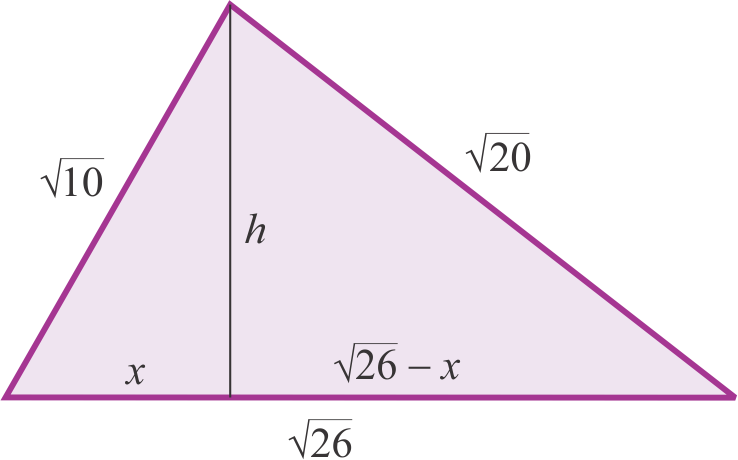
Primjenom Pitagorina poučka na dva pravokutna trokuta, kvadrat visine $h$ iskazuje se na dva načina:
$$
h^2=10-\ x^2\tag{1} \label{1}
$$ $$
h^2=20-\ {(\sqrt{26}-x)}^2.\tag{2}\label{2}
$$
Izjednačavanjem tih izraza za kvadrat visine $h^{2}$ dobiva se jednadžba:
$$
10-\ x^2=20-26+2\sqrt{26}\cdot x-x^2.
$$Njezinim sređivanjem nalazi se vrijednost za $x$:
$$
2\sqrt{26}\cdot x=16
$$ $$
x=\ \dfrac{8}{\sqrt{26}}=\dfrac{4}{13}\sqrt{26}.
$$Uvrštavanjem te vrijednosti u jednadžbu (1) dobiva se vrijednost kvadrata visine:
$$
h^2=10-\dfrac{16\cdot26}{169}=\dfrac{1690-416}{169}=\dfrac{1274}{169},
$$odnosno:
$$
h=\dfrac{\sqrt{1274}}{13}=\dfrac{7\sqrt{26}}{13} .
$$Površina trokuta tada iznosi:
$$
P=\dfrac{1}{2}\cdot \sqrt{26}\cdot \dfrac{7\sqrt{26}}{13}=7.
$$
U drugom članku [2] pokazano je kako je moguće naći površinu raznostraničnog trokuta korištenjem sinusne relacije visine s jednom stranicom i kosinusova poučka. Taj postupak može se ponoviti i kada su stranice kvadratni korijeni, razmatrajući slučaj kad se, na primjer, visina $h$ spušta na stranicu $\sqrt{26}$ (slika 2).
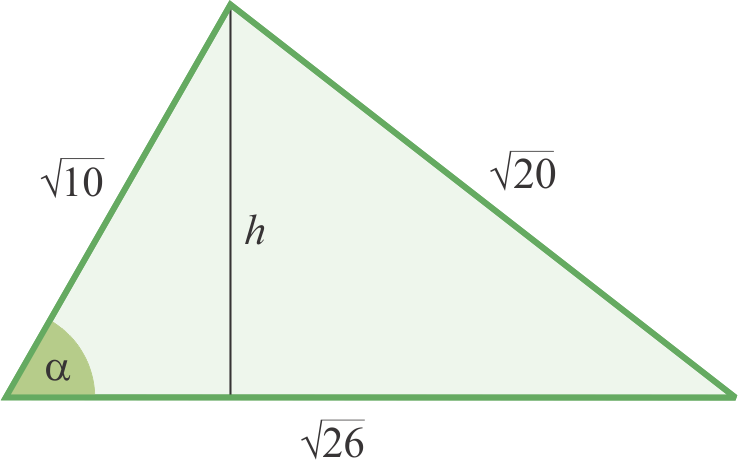
Sinusna relacija visine $h$ uspostavlja se sa stranicom $\sqrt{10}$:
$$
\sin\alpha =\dfrac{h}{\sqrt{10}} .
$$Iz te relacije slijedi:
$$
h=\sqrt{10}\cdot \sin\alpha = \sqrt{10}\cdot \sqrt{1-{\cos}^2\alpha }.\tag{3}\label{3}
$$Primjena kosinusova poučka za kut $\alpha $ daje sljedeću jednadžbu:
$$
20=10+26-2\sqrt{10}\cdot \sqrt{26}\cdot \cos\alpha .
$$Iz nje se dobiva:
$$
\cos\alpha =\dfrac{16}{2\sqrt{260}}=\dfrac{8\cdot \sqrt{260}}{260}=
\dfrac{4\cdot \sqrt{260}}{130}.
$$Kvadrat kosinusa kuta $\alpha $ je:
$$
{\cos}^2\alpha =\dfrac{16\cdot 260}{16\,900}=\dfrac{16}{65},
$$pa je njegov sinus jednak:
$$
\sin\alpha =\sqrt{1-\dfrac{16}{65}}=\sqrt{\dfrac{49}{65}}=\dfrac{7\sqrt{65}}{65}.
$$Uvrštavanjem u jednadžbu (3) dobiva se duljina visine $h$:
$$
h=\ \dfrac{\sqrt{10}\cdot 7\sqrt{65}}{65}=\ \dfrac{7\sqrt{650}}{65}.
$$Površina trokuta jednaka je polovini umnoška stranice $\sqrt{26}$ i visine $h$:
$$
\begin{align}
P&=\dfrac{1}{2} \sqrt{26}\cdot \dfrac{7\sqrt{650}}{65}
=\dfrac{7\sqrt{26\cdot 650}}{130}\\
&=\dfrac{7\sqrt{16\,900}}{130}=\dfrac{7\cdot 130}{130}=7.
\end{align}
$$
Nalaženje površina trokuta s iracionalnim stranicama kao razlike površina pridruženog pravokutnika i triju pravokutnih trokuta
Ovaj je postupak već spomenut u slučaju kada su poznate Kartezijeve koordinate vrhova trokuta [3, 4]. Kako u slučaju razmatranog trokuta sa stranicama $\sqrt{10}$, $\sqrt{20}$ i $\sqrt{26}$ te koordinate nisu poznate, postupak je nešto složeniji. Potrebno je uočiti sljedeće:
- $\sqrt{10}$ je duljina hipotenuze pravokutnog trokuta s katetama duljine 3 i 1.
- $\sqrt{20}$ je duljina hipotenuze pravokutnog trokuta s katetama duljine 4 i 2.
- $\sqrt{26}$ je duljina hipotenuze pravokutnog trokuta s katetama duljine 5 i 1.
Kad se ti pravokutni trokuti ucrtaju u pravokutnik sa stranicama $5$ i $3$, njihove hipotenuze zatvaraju traženi trokut s iracionalnim stranicama $\sqrt{10}$, $\sqrt{20}$ i $\sqrt{26}$ (slika 3).
Površina pridruženog pravokutnika je $15$. Tražena površina trokuta s iracionalnim stranicama dobiva se ako se od te površine oduzme zbroj površina triju pravokutnih trokuta. Te površine imaju sljedeće vrijednosti:
- Površina pravokutnog trokuta s katetama $1$ i $3$ je $1.5$.
- Površina pravokutnog trokuta s katetama $2$ i $4$ je $4$.
- Površina pravokutnog trokuta s katetama $1$ i $5$ je $2.5$.
Kako je zbroj ovih triju površina $8$ ($1.5 + 4 + 2.5 = 8$), površina trokuta sa stranicama $\sqrt{10}$, $\sqrt{20}$ i $\sqrt{26}$ je $7$
($15-8 = 7$).
Nalaženje površine trokuta s iracionalnim stranicama kada su poznate Kartezijeve koordinate njegovih vrhova
Ako su Kartezijeve koordinate vrhova trokuta $ABC$ poznate i iznose $A (x_{1}, y_{1})$, $B(x_{2}, y_{2})$ i $C (x_{3}, y_{3})$, onda je u slučaju kad je poredak vrhova pozitivno orijentiran površina određena formulom [5, 6, 7]:$$
P=\dfrac{1}{2}\ \left|x_1y_2+\ x_2y_3+\ x_3y_1-\ x_2y_1-\ x_3y_2-\ x_1y_3\right|.\tag{4}\label{4}
$$Iz slike 3 je vidljivo da je vrhovima trokuta (sa stranicama $\sqrt{10}$, $\sqrt{20}$ i $\sqrt{26})$ moguće pridružiti sljedeće koordinate (slika 4):
$$
A (0,0),\ B (3,1)\ \text{ i }\ C (1, 5).
$$
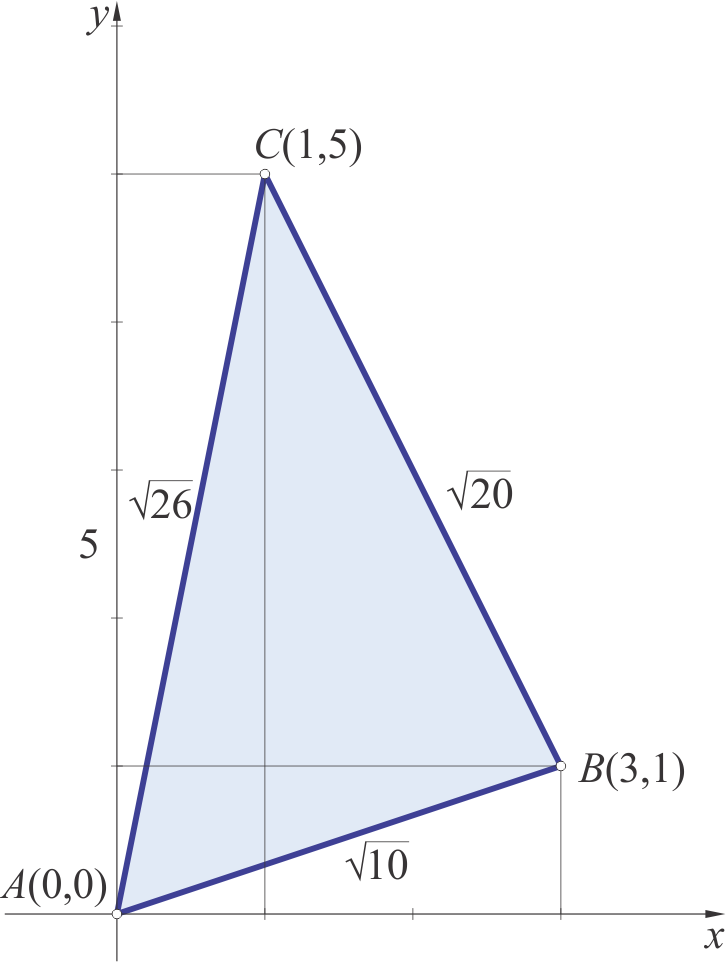
Primjenom formule (4), za slučaj trokuta s duljinama stranicama $\sqrt{10}$, $\sqrt{20}$ i $\sqrt{26}$, dobiva se:
$$
\begin{align}
P&=\dfrac{1}{2} \left(0\cdot 3+3\cdot 5+1\cdot 0-3\cdot 0-1-0\cdot 5\right)\\
&=\dfrac{1}{2}\left(15-1\right)=\dfrac{1}{2}\cdot 14=7.
\end{align}
$$
Nalaženje površine trokuta s iracionalnim stranicama korištenjem Pickove formule
Pickova formula [11] iskazuje površinu mnogokuta $P$ čiji se vrhovi nalaze u čvorovima mreže jediničnih kvadrata, koristeći se brojevima unutrašnjih čvorova ($I$) i rubnih čvorova ($B$):
$$
P=I\ +\dfrac{B}{2}-1.
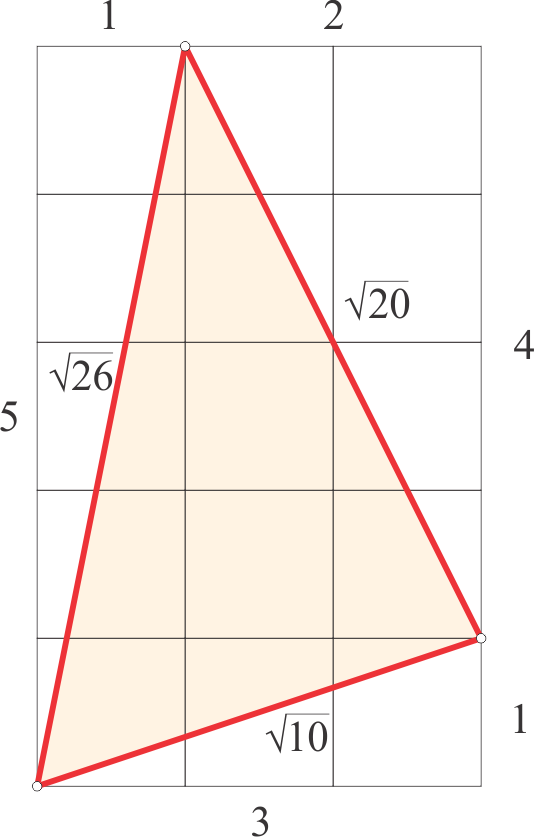
$$Trokut sa stranicama $\sqrt{10}$, $\sqrt{20}$ i $\sqrt{26}$, ucrtan u mrežu jediničnih kvadrata, prikazan je na slici 5.
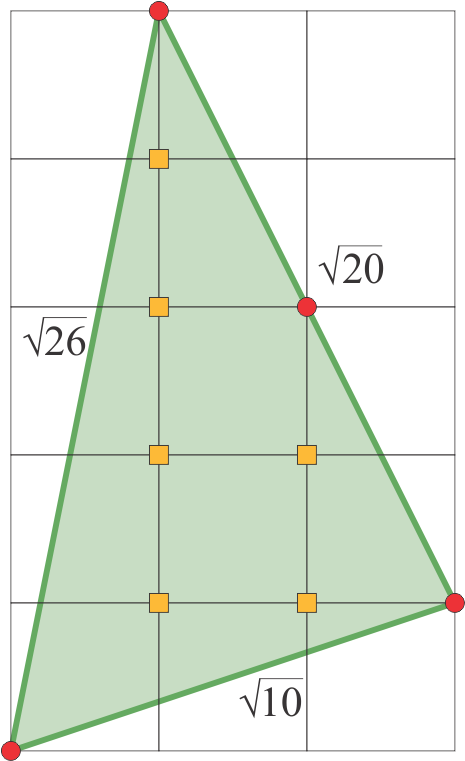
Lako je izbrojiti da je $I$, broj čvorova unutar trokuta označenih ,,kvadratićima”, jednak $6$, a da je $B$, broj rubnih čvorova u vrhovima i na stranicama trokuta označenih ,,kružićima”, jednak $4$.
To znači da je njegova površina:
$$
P=6 +\dfrac{4}{2}-1=6 +2-1=7.
$$
Zaključak
Nalaženje površine raznostraničnog trokuta s iracionalnim stranicama $\sqrt{10}$, $\sqrt{20}$ i $\sqrt{26}$ ima veliki didaktički potencijal jer postoji sedam različitih postupaka rješavanja u kojima se koristimo znanjima iz raznih i, na prvi pogled, nepovezanih područja matematike. Osim što ilustrira ograničenost upotrebe uobičajene verzije Heronove formule, predstavljanje alternativnih načina rješavanja pomoglo bi učenicima u obogaćivanju i integraciji pojmovnih i proceduralnih znanja, što širom otvara vrata razvoju potencijala njihovog kreativnog mišljenja.
Učenicima može biti zanimljiva i naizgled paradoksalna činjenica: površina tog raznostraničnog trokuta s iracionalnim duljinama stranica jest prirodan broj $7$, dok, na primjer, jednakostranični trokut sa stranicama duljine $6$ ima površinu čija je vrijednost iracionalan broj $9\sqrt{3}$.
Važno je napomenuti da prikazani bogat spektar postupaka računanja površine ne postoji u dvije klase raznostraničnih trokuta. U prvom su slučaju duljine stranica cijeli i racionalni brojevi. Na primjer, vrhovi paradigmatičnog povijesnog trokuta sa stranicama $13$, $14$ i $15$ ne mogu imati cjelobrojne Kartezijeve koordinate i ta činjenica smanjuje broj mogućih postupaka za nalaženje njegove površine. To se događa i u drugom slučaju kad su duljine stranica iracionalni brojevi koji nisu kvadratni korijeni iz zbroja kvadrata cijelih brojeva (na primjer, trokut s iracionalnim stranicama $\sqrt{3}$, $\sqrt{7}$ i $\sqrt{11}$).
Tri dodatna primjera raznostraničnih trokuta s iracionalnim stranicama su: $(\sqrt{2}, \sqrt{8}, \sqrt{10})$, $(\sqrt{5},\sqrt{10}, \sqrt{13})$ i $(\sqrt{13},\sqrt{17}, \sqrt{20})$. Svi omogućavaju sedam prikazanih postupaka nalaženja površine trokuta. Zbog toga iznenađuje da je Smith u slučaju posljednjeg trokuta predstavio samo dva načina računanja površine jednake $7$ (,,oduzimanje triju pravokutnih trokuta od četverokuta” i ,,primjena Pickove formule”) [12].
Kreativni izazov za učenike mogu biti zadatci sustavnog istraživanja i pronalaženja novih primjera raznostraničnih, ali i jednakokračnih trokuta s iracionalnim stranicama. Za jednakokračni trokut s iracionalnim stranicama $(\sqrt{20}, \sqrt{10}, \sqrt{10})$, na web-stranici ,,Art of problem solving” navodi se šest mogućih načina rješavanja [13]. Primjena uobičajene inačice Heronove formule detaljno se ilustrira, ali se takav postupak ne preporučuje.
Posebno je važna klasa trokuta s iracionalnim stranicama koji se mogu podijeliti na dva manja trokuta jednakih baza, visina i površina (jedan od njih je, naravno, tupokutan). Primjeri su trokuti sa stranicama $(\sqrt{5},\sqrt{13}, \sqrt{20})$ ili $(\sqrt{13},\sqrt{25}, \sqrt{40})$. Oni omogućavaju iznenađujuće jednostavan osmi postupak nalaženja površine trokuta.
Zanimljivo je da tu mogućnost nalaženja površine u slučaju trokuta s iracionalnim stanicama $(\sqrt{18},\sqrt{34},\sqrt{40})$ realiziranog na mreži jediničnih kvadrata geoploče Sultan i Artzt nisu uočili i predstavili u svojoj knjizi (namijenjenoj srednjoškolskim nastavnicima matematike!) kada su ,,pripremali teren” za uvođenje Pickova teorema [14].
Literatura
- J. Sliško (2023.): Povijest računanja površine trokuta s cjelobrojnim stranicama, Matematika i škola 118, str. 103-109.
- J. Sliško (2023.): Promjena odnosa Heronove formule i računanja površine trokuta s cjelobrojnim stranicama u udžbenicima matematike, Matematika i škola 120, str. 219-224.
- A. L. Griswold, M. L. Keedy i J. F. Schacht (1961.): Contemporary algebra and trigonometry, Holt, Rinehart and Winston, str. 362-363.
- M. L. Keedy, A. L. Griswold, J. F. Schacht i A. Mamary (1967.): Algebra and trigonometry, Holt, Rinehart and Winston, str. 398-399.
- W. E. Byerly (1884.): Syllabus of a course in plane analytic geometry, Ginn, Heath and Company, str. 4.
- S. L. Loney (1895.): The elements of coordinate geometry, Macmillan and Company, str. 16.
- H. B. Fine i H. D. Thompson (1909.): Coordinate geometry, Macmillan, str. 84.
- M. L. Aggarwal (2015.): Learning mathematics. Class X, Avichal Publishing Company, str. 457.
- Varošanec, S. (2019.): Matematika 3. Udžbenik za 3. razred gimnazija i strukovnih škola, Element, str. 5.
- W. Dunham, W. (1990): Journey through genius. The great theorems of mathematics, John Wiley & Sons, str. 128.
- P. L. Cox (1986.): Geometry. An informal approach, Allyn and Bacon, str. 259-260.
- L. R. Smith, (1993.): Multiple Solutions Involving Geoboard Problems, The Mathematics Teacher 86(1), str. 25-29.
- Problem_19(pristupljeno 13.09.2023).
- A. Sultan i A. F. Artzt (2018.): The mathematics every secondary school math teacher needs to know, Routledge, str. 149, slika 4.43.
