Školski kvizovi poboljšavaju obrazovno iskustvo učenika, motiviraju ih za učenje, razvijaju njihove vještine, pomažu u podizanju samopouzdanja i potiču društvene interakcije. Pročitajte kako smo u zagrebačkoj V. gimnaziji potaknuli učenike na osmišljavanje matematičkih zadataka za kviz, a zatim jedan cijeli dan na rješavanje zadataka koje su drugi učenici osmislili.
Ideja
Ideja je nastala u jesen 2021. dok smo intenzivno razmišljali o organizaciji Večeri matematike na razini škole. U to smo doba dolazili u školu pod maskama, a učenici iz različitih razrednih odjela nisu se smjeli miješati. U pretpandemijsko doba organizirali bismo razne radionice, predavanja i radne stanice po cijeloj školi. To ovaj put nije bilo moguće. Svi smo bili siti raznih oblika online aktivnosti, a željeli smo ipak zajedničku aktivnost koja bi povezala učenike s matematikom, ali i učenike međusobno. Osmislili smo jedan specifičan školski kviz.
Naša škola radi u dva turnusa, a u svakom je 14 razrednih odjela. U ovom kvizu nadmetali su se razredi unutar istog turnusa rješavajući zadatke koje su osmislili razredi suprotnog turnusa. Nazvali smo ga ,,Školski pub kviz” zbog kvaliteta koje smo željeli istaknuti – pub kvizovi temelje se na poštenju i povjerenju, nagrade su simbolične, a prestiž i druženje najbitnije su stvari zbog kojih se igraju.
Nakon popuštanja mjera 2022. Večer matematike vratili smo na početne postavke – zagonetke i mozgalice, matematičke igre i matematika iza igara, bijeg iz sobe, radionice i predavanja – za sve učenike po cijeloj školi. Ipak, ideja kviza jako se svidjela i nastavnicima i učenicima pa smo je iskoristili kako bismo obilježili Svjetski dan matematike 2023. (Dan broja $\pi$). Većina zadataka te godine uključivala je broj $\pi $ što je bio zgodan način za tematsko povezivanje kviza s tim danom. Kviz je opet bio uspješan pa smo ga odlučili ponavljati na Dan broja $\pi$ u godinama koje slijede.
Detalji
Organizacija i provedba sastojala se od nekoliko faza:
- Svaki nastavnik svakom razrednom odjelu kojem predaje objašnjava ideju te postavlja rok do kojeg mu trebaju predati svoj razredni zadatak i njegovo rješenje s postupkom u digitalnom obliku. Učenike je potrebno uputiti da razmišljaju o matematičkom zadatku ili pitanju koje je zanimljivo / zabavno / izazovno / iznenađujuće / trik / slabo poznata činjenica. Poželjni su zadatci koji nisu ,,na raspisivanje” već zahtijevaju dobru ideju ili dobru logiku ili dobar zor ili timski rad… Rješenje treba biti kratko. Potrebno je naglasiti da iste zadatke rješavaju učenici od 1. do 4. razreda, pa treba izbjeći specifična znanja viših razreda srednje škole.
- Svaki nastavnik prikuplja zadatke svojih razrednih odjela, provjerava zadovoljavaju li sve postavljene kriterije te ih po potrebi vraća na doradu. Potrebno je provjeriti jasnoću teksta samog zadatka te točnost i jedinstvenost rješenja.
- Prikupljene dorađene zadatke svaki nastavnik šalje koordinatoru kviza. Datoteke su naziva 1A, 1B, 1C itd. prema razrednim odjelima koji su ih osmislili. Koordinator kviza uređuje primljene datoteke, priprema kratka rješenja kako bi se listovi za odgovore mogli brzo ispraviti kada za to dođe vrijeme te obrazac za objavu pobjedničkog odjela.
- Koordinator kviza priprema pano s tablicom zadataka. Za I. turnus tablica sadrži zadatke koje su zadali razredi iz II. turnusa i obrnuto.
- Na dan kviza, prije 1. sata, pano postavljamo na hodnik i ,,otvara se” par zadataka (slika 1). Predstavnik svakog razreda dolazi po list za odgovore (slika 7). Razredi zajedničkim snagama tijekom odmora rješavaju zadatke i odgovore (bez postupka) bilježe na list za odgovore. Tijekom svakog sljedećeg sata ,,otvara se” još nekoliko zadataka tako da učenike tijekom svakog malog odmora dočekaju novi zadatci na panou (slike 4, 6 i 8). Svih 14 zadataka bit će ,,otvoreno” do kraja 3. sata. List s odgovorima potrebno je najkasnije do početka 6. sata ubaciti u kutiju koja se nalazi pored panoa (slika 7).
- Tijekom 6. sata pregledavamo listove s odgovorima i objavljujemo pobjednika plaketom pored panoa (slika 5). Na pano postavljamo raspisana rješenja zadataka (slika 9).









Faza 5. ponavlja se za oba turnusa. U provedbi sudjeluju svi nastavnici matematike prema zaduženjima koje napravi koordinator kviza prateći raspored sati taj dan.
Zabave i natjecateljskog duha nije nedostajalo. Pobjednički razredi dobili su nagradu koja se sastoji od promotivnih materijala škole i matematičkog časopisa za svakog učenika te slatkog razrednog paketa.


Primjeri zadataka
Kako su učenici smišljali zadatke za kviz, tako su zadatke ostalih razreda promatrali očima rješavača, ali i očima sastavljača. Na kraju dana na pano smo postavili sve zadatke iz oba turnusa, a iza svakog zadatka nalazilo se i njegovo rješenje (slika 12). Ovaj pano privlačio je znatiželjnike još danima nakon kviza. Zadatci su analizirani dublje nego što smo to očekivali.


Evo nekoliko primjera zadataka.
1C
Na natjecanju iz matematike upoznale su se 4 učenice: Marija, Jelena, Lidija i Vlatka. One dolaze iz četiri različita grada: Pule, Čakovca, Bjelovara i Trogira. Vlatka i Marija nisu iz Pule, Jelena i Lidija će posjetiti prijateljicu u Bjelovaru, Lidija i Vlatka redovito odlaze na ljetovanje u Trogir, a Marija još nije bila u Čakovcu ni Trogiru. Koja učenica dolazi iz kojeg grada?
2C
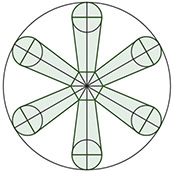
Prozor vitraja na sebi ima ukras u obliku cvijeta od različitih geometrijskih oblika. Ako je promjer okruglog prozora 1 m, duljina stranice pravilnog šesterokuta u sredini 10 cm, a promjer male kružnice 20 cm, kolika je površina ,,cvijeta” na vitrajima? Promjer male kružnice i stranica šesterokuta su paralelni, a promjer prozora dijeli svaku ,,laticu” na točno dva jednaka dijela. Zaokružujte rezultate na dvije decimale i koristite $\pi = 3.14$.
3D
Kako bi satelit prošao jedan puni krug u kružnoj orbiti oko Zemlje, potrebno mu je 120 minuta. Ako je Zemljin polumjer 4000 milja do morske površine,~a satelitska orbita je 400 milja iznad morske razine, koju udaljenost satelit prijeđe u 40 minuta?

4C
Troznamenkasti broj podijeljen zbrojem svojih znamenaka daje količnik 39 i ostatak 2. Koji je to broj ako mu je prva znamenka jednaka prvoj znamenki broja $\pi $ te je zadnja znamenka 4 puta veća od druge?
1E
Istraživači su otkrili novi planet koji je nepravilnog oblika, ali se može aproksimirati kuglom. Zanimalo ih je koliko je puta volumen tog planeta manji od volumena Zemlje. Odabrali su 12 točaka na površini planeta i izračunali udaljenost od središta planeta za svaku točku. Dobili su sljedeće podatke: 327~km, 314~km, 295~km, 312~km, 299~km, 325~km, 320~km, 308~km, 312~km, 318~km, 298~km i 302~km.
Odredi koliko je puta volumen tog planeta manji od volumena Zemlje. Rezultat zaokruži na cijeli broj.
2F
U sljedećem zadatku točnim simbolima popuni prazna mjesta. Sretno!
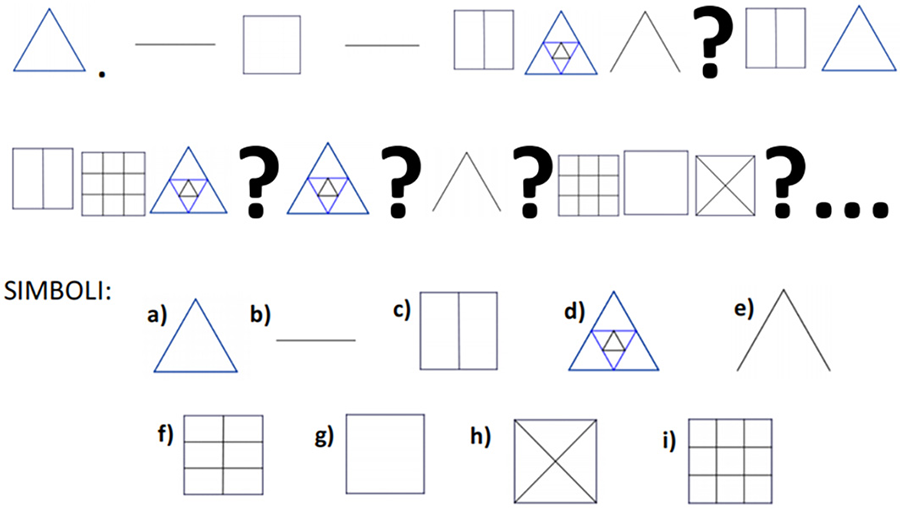
3G
Na slici je stožac kojem je izvodnica dugačka 12~cm. U stošcu je voda.
Ako stožac stoji na svojoj bazi, udaljenost vrha stošca od površine vode iznosi 8~cm. Ako stožac postavimo naopačke, udaljenost baze stošca od površine vode iznosi 2~cm.
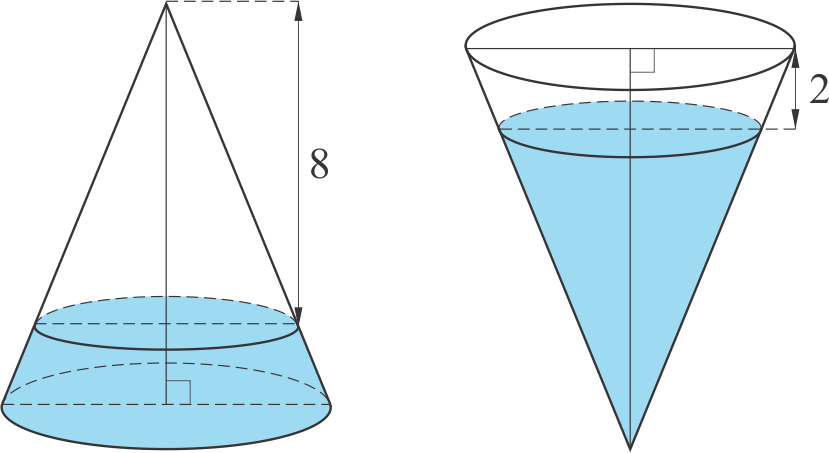
Odredi volumen stošca.
4D
Student se vraća kući s predavanja. Ako je dobre volje, vraća se najkraćim putem. Inače ide u jedan od svojih omiljenih kafića, X, Y ili Z i tamo popije Coca-Colu ili Fantu. Ako mu to podigne moral, ode kući, a inače svrati u još jedan od svojih omiljenih kafića i popije Coca-Colu ili Fantu te nakon toga ode kući.
Koliko ima mogućnosti za put tog studenta kući ako je bitno i što je sve popio?
I mi nastavnici napravili smo analizu riješenosti zadataka. Riješenost izabranih zadataka bila je: 1C – 90 %; 2C – 40 %; 3D – 70 %, 4C – 80 %; 1E – 38 %; 2F – 54 %; 3G – 15 % (ukupno najslabije riješen zadatak); 4D – 92 % (ukupno najbolje riješen zadatak). 1C, 2C, 3D i 4C rješavali su razredi II. turnusa, a 1E, 2F, 3G i 4D razredi I. turnusa.
Analizirali smo i poredak razreda te zaključili da su 3. i 4. razredi donekle u prednosti zbog više znanja, ali i zbog boljih organizacijskih sposobnosti. Taj smo problem naslutili u samom začetku ideje i nakon promišljanja o njemu, zaključili da nam ipak odgovara ovakav koncept kviza. Prvi se razredi tek zagrijavaju i imaju još tri godine da se iskažu i poboljšavaju svoju taktiku iz godine u godinu. Završnim razredima je jako bitno da se istaknu, posebno maturantima koji su jednom nogom van škole i već lagano tuguju zbog rastanka. Razdvajanjem zadataka po razredima niži bi razredi imali bolju šansu za nagradu, a viši bi razredi mogli pokazati i više znanja, no izgubili bi na zajedništvu, a ipak nam je najbitnije bilo pozitivno ozračje u kojem se kviz odigrava. Postoji pregršt događaja u kojima se učenici po razredima natječu u matematičkom znanju. Svjesno smo odlučili izaći iz tog okvira. Iako je u II. turnusu pobijedio 4.F, drugo mjesto su dijelili 1.F, 2.D, 3.F i 4.G.
Zašto je školski kviz dobra ideja?
Ovakvi kvizovi pružaju mogućnost učenicima da prošire svoje znanje iz različitih matematičkih područja. Kroz kvizove učenici mogu naučiti nove činjenice, razumjeti koncepte i povezati informacije, što jača njihovo obrazovno iskustvo. Sudjelovanje u kvizu pomaže u razvoju vještina bitnih za uspjeh u školi, ali i za život. Radi se o vještinama poput brzog razmišljanja, logičkog zaključivanja, kritičkog razmišljanja, rješavanja problema i komunikacijskih vještina. Kvizovi mogu biti izazovni i zabavni, što pomaže učenicima da se motiviraju za učenje. Unošenjem elemenata igre u učionicu stvara se pozitivna atmosfera koja potiče suradnju i timski rad. U ovom kvizu zajedno radi oko 26 učenika i učenica. Bilo je potrebno brzo se i dobro organizirati kako bi se, koristeći samo odmore, što više zadataka uspješno riješilo. Kvizovi pružaju priliku učenicima da pokažu svoje znanje i vještine pred drugima. Ako se učenici uspješno natječu u kvizu i postižu dobre rezultate, to može pridonijeti njihovom samopouzdanju i samopoštovanju. Oni se osjećaju priznatima i motiviranima za daljnji napredak. Možda i najbitnije u postpandemijsko doba, kvizovi mogu stvoriti zajedničko iskustvo i potaknuti društvene interakcije među sudionicima.
