Jednim ravnim rezom pitu možete prerezati na dva komada. Drugi rez, koji siječe prvi, daje četiri komada, a treći rez kao na slici, može dati čak sedam komada. Koliki je najveći broj komada koji se može dobiti sa šest ravnih rezova?
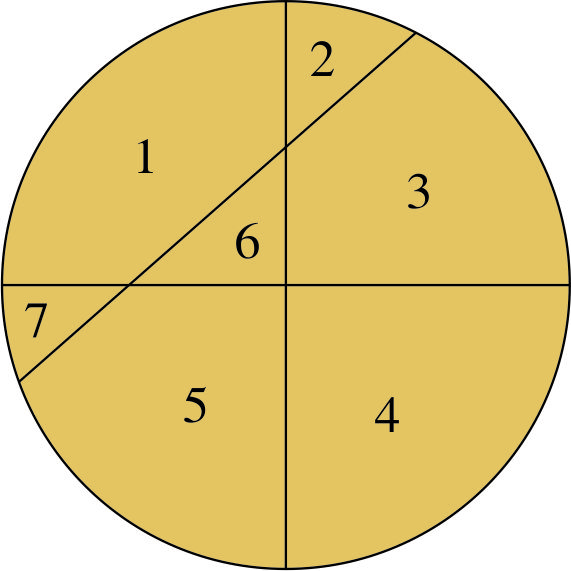
Ovaj se problem može riješiti metodom pokušaja i pogrešaka, no tada skica postaje prilično neuredna i nije osobito poučna. Puno je bolje potražiti pravilo. Razmislimo što se događa kada dodajemo ravne rezove.
Prvi rez dijeli pitu na dva komada.
Drugi rez stvara još dva komada pa ih je ukupno četiri.
Treći rez stvara još tri komada pa ih je ukupno sedam.
Čini se da svaki rez povećava ukupan broj komada za broj koji odgovara rednom broju reza. Dakle, četvrti rez može stvoriti najviše četiri nova komada, peti rez pet, a šesti rez šest. Najveći mogući broj komada je, dakle, 22.
Sada lako dolazimo do opće formule za najveći broj komada $P(n)$ koje možete dobiti s $n$ ravnih rezova:$$P(n)=1+\frac{n(n+1)}{2}.$$
Drugim riječima, dodajemo 1 (početni komad) zbroju svih brojeva od $1$ do $n$. Odnosno pogledajmo na primjeru
- $P(1)=1+\frac{1\cdot2}{2}=2$
- $P(2)=1+\frac{2\cdot3}{2}=4$
- $P(3)=1+\frac{3\cdot4}{2}=7$
- $P(6)=1+\frac{6\cdot7}{2}=22$.
Učenje temeljeno na zagonetkama
Gornju zagonetku postavio je Martin Gardner [2], matematičar koji je osmislio mnoge zagonetke, paradokse i matematičke igre. Rješavanje zagonetki, poput gornje, pokazuje kako i jednostavan problem može potaknuti razmišljanje, prepoznavanje uzoraka i formuliranje općeg pravila. Iskustva u kojima učenici aktivno istražuju, postavljaju hipoteze i nailaze na aha-doživljaje, čine srž pristupa poznatog kao učenje temeljeno na zagonetkama (engl. Puzzle-Based Learning). Takva nastavna metoda naglašava aktivno i problemski orijentirano učenje pri čemu zagonetke služe kao alat za razvoj kritičkog i kreativnog mišljenja, logičkog zaključivanja i motivacije za istraživanje.
Jedna od poznatijih zagonetki jest zagonetka o čokoladnoj pločici: pravokutnu pločicu potrebno je razlomiti na $m\times n$ jednakih kvadratnih dijelova s najmanjim mogućim brojem koraka, no u svakom se koraku pločica može razlomiti po jednoj liniji. Rješenje zahtijeva prepoznavanje uzorka – svako lomljenje povećava broj komada za jedan, što dovodi do općeg pravila da je potreban $mn-1$ korak. Ovaj zadatak uvodi učenike u matematičko modeliranje i strategije poput načela invarijance i matematičke indukcije, pokazujući kako se heurističko razmišljanje može formalizirati u dokaz. Zagonetke je korisno ubaciti u nastavu matematike jer pomažu učenicima vidjeti da matematika nije samo računanje nego i analiza, modeliranje i otkrivanje pravilnosti. Potiče korištenje heuristika (npr. rastavi problem na manje dijelove, razmišljaj unatrag), koje su temeljne za rješavanje složenijih problema iz algebre, analize ili statistike.
Što je to zagonetka?
Kako bismo mogli govoriti o učenju temeljenom na zagonetkama, moramo najprije razjasniti što je to zagonetka. Zagonetka je svima opće poznati pojam, ali zanimljivo je kako ne postoji jednoznačna definicija iste. Iako ne postoji dogovorena definicija, moglo bi se reći:
Zagonetka je pitanje ili izričaj skrivena ili dvosmislena značenja postavljeno kao problem koji valja riješiti. (Hrvatska enciklopedija)
Također, može se reći da su zagonetke pitanja koja potiču na razmišljanje, predstavljaju izazov za našu maštu te traže primjenu kreativnog i kritičkog mišljenja. Ako zadatak shvatimo kao sveobuhvatni pojam za svaku aktivnost zadanu učeniku, tada u literaturi možemo pronaći brojne izraze koji opisuju specifične vrste zadataka, uključujući vježbu, problem i zagonetku, koji se ponekad upotrebljavaju kao sinonimi. U nastavku rada objasnit ćemo razlike između vrsta zadataka te dati primjer za svaku od kategorija.
Vježba je zadatak, bio on jednostavan ili nešto složeniji, koji se može riješiti rutinski primjenom naučene metode.
Zadatak 1. Izračunaj $\dfrac12+\dfrac25$.
Učeniku koji nije učio kako se zbrajaju razlomci ovo može predstavljati problem, no za ostale učenike osnovne i srednje škole riječ je o jednostavnoj vježbi.
Problem je više od vježbe. Problemski su zadatci u matematici vrlo često zadani riječima te matematika u pozadini nije uvijek očita. Iako možda nije vidljivo odmah kako pristupiti rješavanju problema, učenici moraju zaključiti što problem zapravo predstavlja, izdvojiti važne informacije te odrediti kako ih matematički prikazati. Prethodno opisano naziva se matematičko modeliranje.
Zadatak 2. Riješi sljedeći zadatak: “Na Fakultetu primijenjene matematike ima šest puta više studenata nego što ima profesora.” Za broj studenata koristi se oznakom $S$, a za broj profesora oznakom $P$.
Iskustvo samog učenika značajno utječe na to hoće li određeni zadatak percipirati kao vježbu ili kao problem. No vrlo često učenici zapisuju ovaj problem kao $6S=P$ i dolaze do netočnog rješenja. Upravo prijelaz s problema danog riječima na njegov matematički prikaz može nerijetko predstavljati izazov učenicima i zbog toga gornji zadatak možemo promatrati kao problem.
Prema Michalewicz & Michalewicz [6], zagonetka je ono što zadovoljava četiri kriterija:
- općenitost (objašnjava neko univerzalno matematičko načelo rješavanja problema)
- jednostavnost
- trenutak spoznaje i
- zabavu.
Kako su autori naglasili, općenitost je i karakteristika problema, a ne samo zagonetki. Također, ni sve zagonetke nisu nužno jednostavne. S obzirom na preostale kriterije zagonetku možemo opisati kao problem koji zbunjuje i čije rješenje zahtijeva domišljatost te često dovodi do neočekivanog, ponekad i neintuitivnog zaključka [5]. Rješavanje neke zagonetke često rezultira tzv. aha-trenutkom koji daje visoku razinu intelektualnog zadovoljstva. Zbog toga zagonetke zapravo možemo promatrati kao podvrstu problema, a učenje koje se temelji na rješavanju problema u velikoj mjeri sadržava i rješavanje zagonetki.
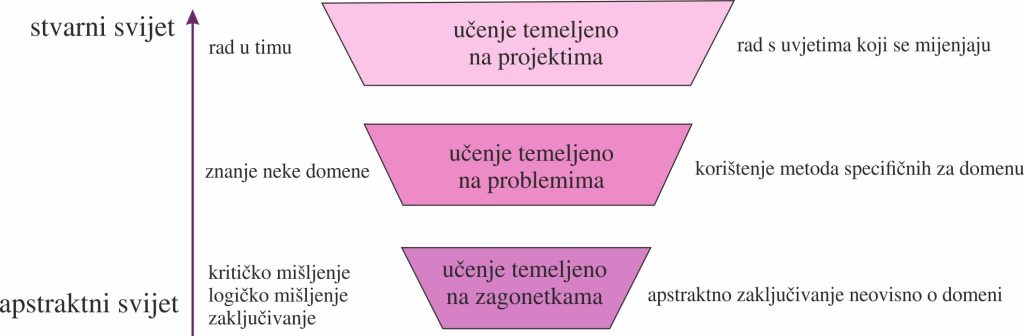
Model prikazan na slici pozicionira učenje temeljeno na zagonetkama na najapstraktnijem dijelu kontinuuma između apstraktnog i stvarnog svijeta, gdje učenici bez pritiska stvarnih posljedica razvijaju strategije rješavanja problema [5]. Učenje temeljeno na problemima nadovezuje se na to primjenom strategija u specifičnim domenama, a projektno učenje vodi do rješavanja stvarnih, složenih izazova. Time učenje temeljeno na zagonetkama čini prvu stepenicu u izgradnji matematičke pismenosti i sposobnosti kritičkog razmišljanja.
Zadatak 3. Dijagonale dviju susjednih strana kocke sastaju se u vrhu. Koliko iznosi kut između dijagonala?
Ovaj zadatak može se shvatiti kao primjer problema koji se može riješiti trigonometrijom ili vektorima. No, odmaknemo li se od trigonometrijskog načina razmišljanja, primjećujemo da spojimo li preostale krajnje točke dijagonala, dobijemo jednakostranični trokut te zaključujemo kako je kut između dijagonala jednak 60°. Budući da se zadatak može riješiti i intuitivno, poprima obilježja zagonetke – sadržava trenutak spoznaje (aha-trenutak) te pruža osjećaj intelektualnog zadovoljstva pri rješavanju.
Kako rješavati zagonetke?
Učenje temeljeno na zagonetkama vrlo je učinkovit način za razvoj kritičkog mišljenja, ustrajnosti i strategija rješavanja problema. Za razliku od rutinskih zadataka zagonetke su nestrukturirane, često kontekstualno neutralne i ne zahtijevaju posebno stručno predznanje, a pritom potiču znatiželju i osjećaj postignuća. Njihova vrijednost nije samo u zabavi nego i u tome što uvode učenike u proces matematičkog razmišljanja i to promatranje uzoraka, formuliranje hipoteza, izgradnju modela i dokazivanje.
Tijekom godina razvijeni su brojni pristupi rješavanju problema, a jedan od najutjecajnijih opisao je György Pólya u svojoj klasičnoj knjizi Kako riješiti matematički zadatak. Pólya razlikuje četiri temeljna koraka:
- Razumijevanje problema – precizno odrediti što se traži i koje su dane informacije.
- Planiranje rješenja – osmisliti strategiju, povezati problem s poznatim rezultatima i pronaći moguće pristupe.
- Provođenje plana – sustavno provesti odabranu strategiju i izračune.
- Provjera – analizirati dobiveni rezultat, provjeriti njegovu logičnost i eventualno ga generalizirati.
Pólyin popis heuristika uključuje tehnike poput traženja invarijanti, razmatranja ekstremnih slučajeva, rastavljanje problema na manje dijelove ili razmišljanja unatrag. Sve su to strategije koje se kasnije pojavljuju i u formalnoj matematici npr. u kombinatorici, algebri ili teoriji optimizacije. Michalewicz i Michalewicz [6] predložili su pojednostavnjeni, ali vrlo praktičan postupak koji posebno naglašava modeliranje:
- Razumijevanje problema – precizno definirati sve pojmove i izraze.
- Provjera intuicije – ne oslanjati se isključivo na dojam; primjenjivati provjerljive izračune.
- Izgradnja modela – odrediti varijable, ograničenja i ciljeve te stvoriti matematički ili logički model problema.
Ovaj pristup od učenika traži razvoj discipliniranog načina razmišljanja slično onome kojim se koriste matematičari. Modeliranje je ključni korak jer omogućuje da se čak i naizgled zabavna zagonetka pretvori u vježbu iz logičkog zaključivanja i apstraktnog razmišljanja.
Metode rješavanja zagonetki
U ovome dijelu prikazat ćemo neke metode za rješavanje zagonetki koje mogu pomoći učitelju razumjeti kako one mogu biti primijenjene u učionici. Promotrimo jednu od najvećih prepreka za učenika: otkrivanje što je zapravo problem kako bi se u konačnici on mogao i riješiti. Budući da problem nije uvijek očit te ne postoji univerzalni način rješavanja svih problema, korisno je imati strategiju koja nam može olakšati dolazak do rješenja. To možemo učiniti na nekoliko načina: napraviti popis činjenica, postaviti matematički model ili crtati dijagram.
Zadatak 4. Seljak mora prevesti vuka, kozu i kupus preko rijeke, ali ima čamac koji može primiti samo njega i još jedan predmet. Ako ostavi vuka i kozu same, vuk će pojesti kozu. Slično, ako koza i kupus ostanu sami bez seljaka – i ako koza već nije pojedena – koza će pojesti kupus. Kako seljak može sigurno prevesti sve na drugu obalu? Seljak mora biti u čamcu da bi ga mogao prevesti s jedne strane na drugu.
Popis činjenica:
- Seljak mora biti u čamcu da bi mogao prevoziti.
- U čamcu mogu biti samo dva objekta, od kojih jedan mora biti seljak.
- Vuk i koza ne mogu biti ostavljeni zajedno bez nadzora seljaka.
- Koza i kupus ne mogu biti ostavljeni zajedno bez nadzora seljaka.
- Vuk i kupus mogu ostati zajedno bez nadzora.
Izdvajajući sve činjenice ove zagonetke, može se jasno vidjeti koji su uvjeti i ograničenja rješenja te se time eliminiraju neke mogućnosti. Ovaj problem najbolje je riješiti grafički (crtanjem dijagrama). Koristit ćemo se tablicom u kojoj ćemo prikazati svaki korak pri rješavanju problema. Jedno od rješenja problema možete vidjeti u sljedećoj tablici.
TABLICA
| korak | lijeva obala | u čamcu (→ ili ←) | desna obala |
| 1 | seljak, vuk, kupus | seljak + koza → | koza |
| 2 | vuk, kupus | seljak ← | koza |
| 3 | kupus | seljak + vuk → | vuk, koza |
| 4 | seljak + koza, kupus | seljak + koza ← | vuk |
| 5 | koza | seljak + kupus → | vuk, kupus |
| 6 | koza | seljak ← | vuk, kupus |
| 7 | – | seljak + koza → | vuk, kupus, koza |
Prepoznavanje uzoraka
Sposobnost ljudskog uma da prepoznaje uzorke iznimno je korisna pri rješavanju različitih problema. Međutim, često vidimo uzorke i ondje gdje ih zapravo nema. Stoga prepoznavanje uzoraka može biti jednako korisno koliko i varljivo. Nakon što uočimo uzorak, moramo procijeniti je li on stvaran ili samo prividan. Sljedeća zagonetka može poslužiti kao dobar uvod u prepoznavanje uzoraka.
Zadatak 5. Nizu od četveroznamenkastih brojeva pridružen je jednoznamenkasti broj. Primjer takvog pridruživanja nalazi se u nastavku:
| 8809 | 6 |
| 7111 | 0 |
| 2172 | 0 |
| 6666 | 4 |
| 1111 | 0 |
| 3213 | 0 |
| 7662 | 2 |
| 9313 | 1 |
| 0000 | 4 |
| 3333 | 0 |
| 8193 | 3 |
| 8096 | 5 |
| 7777 | 0 |
| 9999 | 4 |
| 7756 | 1 |
| 6855 | 3 |
Koji broj treba biti pridružen broju 2581?
Na prvi pogled, riječ je o nasumičnom nizu brojeva. Ono što ovaj zadatak čini zanimljivim jest činjenica da će obrazovanijim osobama često trebati više vremena da pronađu rješenje. Zašto? Zato što problemu pristupaju analitički – pokušavaju naći neku matematičku logiku u pozadini, uzorke i pravilnosti u nizu. S druge strane, učenici mlađe dobi, koji se oslanjanju na vizualno opažanje, brže dolaze do zaključka jer promatraju same oblike znamenaka i brojeva, a ne njihovu matematičku vrijednost.
Rješenje ovog zadatka je zapravo vrlo jednostavno i očito. Svakom četveroznamenkastom broju pridružuje se vrijednost na osnovi broja zatvorenih kružnih oblika u njegovom vizualnom prikazu. Tako je, na primjer, brojevima koji sadrže samo znamenke 1, 2, 3, 5 i 7 pridružena vrijednost 0 jer ne sadrže niti jedan krug. Suprotno tome, brojevi 0, 6 i 9 imaju vrijednost 1, dok broj 8 ima vrijednost 2. Testiramo li ovaj zaključak na nekom od primjera, zaista uočavamo kako je riječ o točnoj ideji te zaključujemo da je rješenje zadatka sljedeće: “Broju 2581 treba biti pridružen broj 2.”
Sljedeći problem ilustrira kako zagonetka može tražiti primjenu informacije koja je većini poznata, ali na koju zaborave upravo onda kada je trebaju primijeniti.
Zadatak 6. Koje slovo (označeno s ?) nedostaje u danom nizu: A ? D F G H J K L
Budući da je rješenje ovog zadatka zaista jednostavno, rješavanje istog ostavljamo čitatelju za zabavu.
Numeriraj i eliminiraj
Jedna od najpoznatijih metoda koja je primjenjiva na mnoge probleme temelji se na označavanju (numeriranju) svih mogućih rješenja problema i sustavnoj eliminaciji svih pogrešnih rješenja. Ponavljanje ovog procesa eliminacije postupno sužava izbor, sve dok ne ostane skup potencijalno točnih rješenja. Upravo je ovu metodu često primjenjivao i Sherlock Holmes, što može biti zanimljivo prilikom uvođenja metode u nastavu. Naravno, ispisivanje svih mogućnosti ponekad može biti opširan i zamoran zadatak, ali ne mora to uvijek biti tako. Sljedeća zagonetka prikladna je za uvođenje učenika u način razmišljanja prilikom primjene metode.
Zadatak 7. Gospodin Smeđi, gospodin Bijeli i gospodin Zeleni nalaze se u trgovini šešira i žele kupiti šešire različitih boja. Izlazeći iz trgovine nakon kupovine, osoba sa zelenim šeširom rekla je : “Jeste li primijetili da iako boja naših šešira odgovara našim imenima, niti jedan od nas nema šešir iste boje kao njegovo ime?” Gospodin Smeđi je odgovorio: “Zaista, u pravu si. Čudesno!” Koje su boje šeširi svakog od njih?
Ovo je dobar primjer problema koji lijepo ilustrira proces eliminacije nakon što se sve mogućnosti označe. Da bismo to učinili, uvedimo sljedeće oznake: S, B i Z redom za boje smeđa, bijela i zelena. Ako ne znamo ništa osim toga da su 3 gospodina izabrala boju šešira od ove 3 s popisa, model bi izgledao ovako:
| gosp. Smeđi: | S ili B ili Z |
| gosp. Bijeli: | S ili B ili Z |
| gosp. Zeleni: | S ili B ili Z |
Kako niti jedna boja šešira ne odgovara prezimenu osobe koja ga nosi (prvi uvjet), moguće je eliminirati nekoliko mogućnosti:
| gosp. Smeđi: | B ili Z |
| gosp. Bijeli: | S ili Z |
| gosp. Zeleni: | S ili B |
Pogledamo li drugi dio zadatka, u kojem je osoba sa zelenim šeširom rekla nešto, na što je odgovorio gospodin Smeđi, zaključujemo da gospodin Smeđi nema zeleni šešir:
| gosp. Smeđi: | B |
| gosp. Bijeli: | S ili Z |
| gosp. Zeleni: | S ili B |
Prethodno daje:
| gosp. Smeđi: | B |
| gosp. Bijeli: | S ili Z |
| gosp. Zeleni: | S (jer znamo da gosp. Smeđi nosi bijeli šešir) |
što dalje povlači:
| gosp. Smeđi: | B |
| gosp. Bijeli: | Z (jer gosp. Zeleni nosi smeđi šešir) |
| gosp. Zeleni: | S |
Ovo u konačnici daje sljedeći zaključak: Gospodin Smeđi nosi bijeli šešir, gospodin Bijeli nosi zeleni šešir i gospodin Zeleni nosi smeđi šešir.
Neki učenici mogu imati poteškoća pri rješavanju problema ovog tipa jer misle da im nije dovoljno informacija na raspolaganju. No, ovo je zanimljiva zagonetka koja se na prvu čini nemoguća za riješiti, ali ako ispišemo sve mogućnosti, postaje poprilično jednostavna.
Pojednostavnjivanje
Značajni dio uspješnog rješavanja problema svodi se na primjenu strategija koje čine rješenje dostupnijim. Pojednostavnjivanje problema jedna je od takvih strategija. Postoji mnogo načina na koji se problem može pojednostavniti kako bi se lakše došlo do rješenja. Primjerice, može se dani problem preformulirati ili promijeniti u oblik koji je razumljiviji. Drugi način pojednostavnjivanja jest rješavanje pojednostavnjene inačice složenijeg problema. To često omogućava bolje razumijevanje i uvid u strukturu samog problema, što može voditi prema njegovu rješenju. Ipak, veoma je važno da pritom ne izgubimo iz vida koji je zapravo problem koji pokušavamo riješiti. Također, jedan od načina može biti i pretpostavljanje neke informacije koja nedostaje i rješavanje problema s tom pretpostavkom, što je svakako korak prema rješenju početnog problema. Općenitog načina za pojednostavnjivanje problema nema, ali postoje neki koraci koji se mogu primijeniti na svaki problem:
1. Može li se problem svesti na puno manji problem i tako riješiti početni problem?
2. Može li se promijeniti način na koji predstavljamo problem?
3. Može li se izvršiti redukcija problema?
Pogledajmo primjenu ovih načela na sljedećem primjeru.
Zadatak 8. Osoba stoji ispred slike čovjeka i kaže: “Braće i sestara nemam, ali otac ovog čovjeka sin je mog oca.” Tko je na slici?
Učenici često moraju pročitati ovaj problem više puta prije nego li mogu krenuti na rješavanje. Naravno, nerijetko će učenici ponuditi neki pretpostavljeni odgovor, ali bez objašnjenja. Cilj je potaknuti učenike na razmišljanje, a ne na pogađanje rješenja. Problem postaje puno jednostavniji kada frazu “sin mog oca” zamijenimo jednostavnijom frazom koja može biti ili „ja (muška osoba)“ ili „moj brat“. Dakle, pojednostavnjena inačica problema glasila bi ili “Braće i sestara nemam, ali otac ovog čovjeka sam ja” ili “Braće i sestara nemam, ali otac ovog čovjeka je moj brat”. Zbog prvog uvjeta druga inačica nije moguća i iz pojednostavnjenog problema jasno je da je čovjek na slici sin osobe koja gleda sliku.
Zagonetke u nastavi matematike
Različita istraživanja potvrđuju učinkovitost učenja temeljenog na zagonetkama u nastavi matematike. Ovdje ćemo istaknuti istraživanja vezana za visokoškolsku nastavu matematike kako bismo pokazali da ovo zaista nije neozbiljna metoda. Thomas i sur. [7] integrirali su zagonetke unutar kolegija o matematičkim modelima za studente tehničkih studija. Jedna do dvije zagonetke pojavljivale su se unutar seta od 10 do 12 zadataka. Na taj način zagonetke su kontinuirano bile dio procesa učenja. Istraživanje je pokazalo kako primjena zagonetki značajno povećava angažman i motivaciju, a studenti su izjavili da zagonetke potiču aha-trenutke i olakšavaju prijelaz s učenja napamet na bolje razumijevanje matematičkih modela. Slične rezultate donosi i studija Klymchuka [3], provedena sa studentima druge godine tehničkih studija, u kojoj je predavač unutar kolegija funkcija više varijabli tijekom šest tjedana redovito uključivao 2–3 zagonetke po predavanju uz raspravu u paru ili grupi. U toj studiji čak 97 – 98 % ispitanika izjavilo je kako rješavanje zagonetki poboljšava njihove vještine rješavanja problema i generičkog razmišljanja. Osim toga, 82 % studenata navelo je dodatne koristi poput zabave, mentalne pauze i veće koncentracije, dok su najčešći komentari upućivali na razvoj kreativnosti i fleksibilnosti u razmišljanju (“thinking outside the box”).
U jednoj osnovnoj školi Osječko-baranjske županije provedeno je istraživanje s učenicima sedmih i osmih razreda [8]. Učenici su anonimno ispunjavali upitnik koji je sadržavao tri zagonetke obrađene u članku (Zadatak 5, 7 i 8). Nakon svake zagonetke ostavljen je prostor u koji su učenici mogli zapisati svoj postupak rješavanja i konačni odgovor. Ovo malo istraživanje pokazalo je da učenici imaju poteškoća u rješavanju zagonetki, ali i da takvi zadatci potiču njihovu znatiželju i motivaciju. Učenici su Zadatak 8 često smatrali najlakšim, iako su pri rješavanju griješili, dok je Zadatak 7 bio ocijenjen kao najteži zbog duljeg teksta i zbunjujuće formulacije. Kod Zadatka 5 većina učenika tražila je matematičko pravilo umjesto vizualnog, što upućuje na preveliko oslanjanje na naučene algoritme i nedostatak fleksibilnosti u razmišljanju. Rezultati upućuju na potrebu da učenici budu sustavno izloženi problemskim situacijama koje traže kreativno razmišljanje, analizu i ustrajnost – što je i jedan od ciljeva nastave matematike. Učenje temeljeno na zagonetkama može biti vrijedan alat jer stavlja učenike u istraživačku poziciju, potiče razvoj vlastitih strategija i učenje iz pokušaja i pogrešaka. Osim razvoja logičkih i matematičkih vještina ovakav pristup jača samopouzdanje u suočavanju s nepoznatim problemima te motivira učenike za daljnje učenje.
Osim što može biti zabavno, učenje temeljeno na zagonetkama može uvjeriti učenike da [1]:
- znanost može biti korisna i zanimljiva
- matematika nije strašna (nema razloga za mržnju prema njoj)
- vrijedi ostati u školi, završiti studij i zakoračiti u stvarni svijet koji je prepun zanimljivih problema (problema koji se mogu promatrati kao zagonetke iz stvarnog života).
Primjeri nekih zagonetki
I za kraj nekoliko zagonetki koje pokušajte riješiti sami:
Zagonetka 1 [4]. Zadana je jednakost koju čini 12 šibica. Jednakost pokazuje: $6-4=9$. Pomakni samo jednu šibicu kako bi dobio istinitu jednakost.
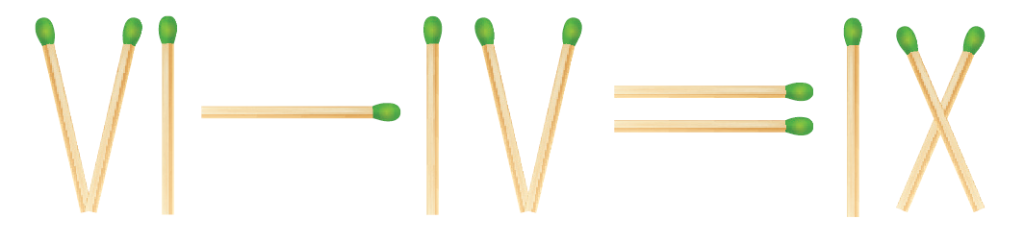
Zagonetka 2 [5]. Na stolu se nalaze čaša soka i čaša vode jednakog volumena. Uzmemo punu žlicu soka i prelijemo je u čašu s vodom. Nakon što smjesu kratko promiješamo, ponovno uzmemo punu žlicu tekućine iz čaše s vodom i vratimo je u čašu sa sokom. Pitanje glasi: čega je na kraju više – soka u čaši vode ili vode u čaši soka?
Zagonetka 3 [5]. Na vinovoj lozi dugoj 2 metra nalazi se 100 mrava. Šezdeset ih gleda ulijevo, a četrdeset udesno. Svaki mrav kreće se konstantnom brzinom od 2 cm/s. Kada se mravi sudare na lozi, odmah promijene smjer. Ako stignu do jednog kraja loze, silaze s loze i nastavljaju dalje. Koliko najduže možeš čekati dok svi mravi ne napuste lozu?
Literatura
- T. Evans, M. O. J. Thomas & S. Klymchuk (2021.): Non-routine problem solving through the lens of self-efficacy. Higher Education Research & Development, 40(7), 1382–1397. https://doi.org/10.1080/07294360.2020.1818061
- M. Gardner (1986.): Entertaining mathematical puzzles. Dover Publications.
- S. Klymchuk (2017.): Puzzle-based learning in engineering mathematics: Students’ attitudes. International Journal of Mathematical Education in Science and Technology, 48(7), 1106–1119. https://doi.org/10.1080/0020739X.2017.1327088
- B. A. Kordemsky (1992.): The Moscow puzzles: 359 mathematical recreations. Dover Publications
- G. Meyer, L. Falner, R. Sooriamurthi & Z. Michalewicz (2014.): Guide to teaching puzzle-based learning. Springer-Verlag.
- Z. Michalewicz, & M. Michalewicz (2008.): Puzzle-based learning: An introduction to critical thinking, mathematics, and problem solving. Hybrid Publishers
- C. Thomas, M. Badger, E. Ventura-Medina & C. Sangwin (2013.): Puzzle-based learning of mathematics in engineering. Engineering Education, 8(1), 122–134. https://doi.org/10.11120/ened.2013.00005
- A. Živković (2025.): Učenje temeljeno na zagonetkama (Diplomski rad). Sveučilište Josipa Jurja Strossmayera u Osijeku, Fakultet primijenjene matematike i informatike.
