Vjerojatnost u razrednoj nastavi matematike
– iz aspekta udžbenika

U ovom radu problematizira se uvođenje sadržaja iz vjerojatnosti u razrednu nastavu matematike iz aspekta obrazovanja učitelja te udžbeničkih sadržaja. Naime, mnogi učitelji razredne nastave tijekom svojeg formalnog obrazovanja nikada nisu učili o vjerojatnosti niti metodici nastave vjerojatnosti, a te sadržaje sada trebaju poučavati. Stoga smo se pitali kakvu podršku učiteljima pružaju matematički udžbenici, odnosno kakva je ponuda i zastupljenost ovakvih zadataka.

Uvod

Uvođenjem novog Kurikuluma nastavnog predmeta Matematika za osnovne škole i gimnazije (Ministarstvo znanosti i obrazovanja [MZO], 2019) sadržaji iz statistike i vjerojatnosti uključeni su i u razrednu nastavu matematike – putem domene E. Domena E – Podatci, statistika i vjerojatnost obuhvaća učeničke aktivnosti prikupljanja, razvrstavanja, obrađivanja, analiziranja te prikazivanja podataka. Također, kod učenika se želi potaknuti upotreba statističkog rječnika te usvajanje pojmova iz područja vjerojatnosti (MZO, 2019).

Ishodi iz vjerojatnosti u razrednoj nastavi

Ako usporedimo broj ishoda kurikuluma među različitim domenama, zaključit ćemo da je domena Podatci, statistika i vjerojatnost vrlo malo zastupljena u razrednoj nastavi u odnosu na broj ishoda ostalih domena. Gledajući cjelokupnu domenu E, u kurikulumu se nalazi samo po jedan odgojno-obrazovni ishod iz te domene za prvi i treći razred, dok se za drugi i četvrti nalaze po dva odgojno-obrazovna ishoda (MZO, 2019). Dok su ishodi iz statistike prisutni u sva četiri razreda (u svakom razredu po jedan ishod), iz vjerojatnosti u razrednoj nastavi nailazimo samo na dva ishoda, i to jedan u drugom, a jedan u četvrtom razredu (tablica 1).

RAZRED	ODGOJNO-OBRAZOVNI ISHOD	RAZRADA ISHODA
2.	MAT OŠ E.2.2. Određuje je li neki događaj moguć ili nemoguć.	U različitim situacijama predviđa moguće i nemoguće događaje. Objašnjava zašto je neki događaj (ne)moguć.
4.	MAT OŠ E.4.2. Opisuje vjerojatnost događaja.	U razgovoru iskazuje mogućnosti. Uspoređuje ishode riječima vjerojatniji, manje vjerojatan, najvjerojatniji.

Prema ishodu MAT OŠ E.2.2. učenici u drugom razredu određuju je li neki događaj moguć ili nemoguć. Preporuka koja je navedena u kurikulumu glasi: „Ovaj je ishod priprema učenika za razumijevanje i primjenu pojma vjerojatnost kako bi osvijestili da neki događaj ili pojava mogu završiti različitim ishodima te kako bi se osposobili za pravilnu upotrebu riječi moguće ili nemoguće“ (MZO, 2019, str. 33). Sadržaj iz vjerojatnosti ponovno se pojavljuje u četvrtom razredu pod ishodom MAT OŠ E.4.2. gdje učenici opisuju i uspoređuju vjerojatnost događaja uz primjenu izraza kao što su: vjerojatniji, manje vjerojatan  i najvjerojatniji. Također, učenici trebaju razumjeti razliku između ishoda događaja koji je siguran, moguć i nemoguć (MZO, 2019).

Jasno je da u razrednoj nastavi učenici neće računati vjerojatnost događaja koji se prikazuje postotkom ili decimalnim brojem, već je ovdje cilj procjena je li događaj moguć, nemoguć ili siguran te poticanje učenika na objašnjavanje konkretnim primjerima i iskustvom (Loparić, 2019; Soucie, 2011). Također, očekuje se i usporedba takvih procjena ishoda uz primjenu izraza vjerojatniji, manje vjerojatan, najvjerojatniji, najmanje vjerojatan i sl. Takve aktivnosti i procjene svakako čine važan temelj za kasnije računanje vjerojatnosti sigurnog događaja. Kako navodi Huzak (2005), bitno je da se ključni pojmovi vjerojatnosti uvode postupno uz pomoć primjera i analiza slučajnih događaja. To je u skladu sa stupnjevima učenja pojmova iz vjerojatnosti (Polaki, 2002):

1. stupanj – učenici predviđaju vjerojatnost na temelju subjektivnog doživljaja
2. stupanj – učenici predviđaju najvjerojatnije i najmanje vjerojatne događaje
3. stupanj – učenici točno predviđaju vjerojatnost događaja te pritom upotrebljavaju brojeve
4. stupanj – učenici određuju točnu vjerojatnost događaja.

No, ovdje se javlja jedan praktični problem, obzirom da se radi o novim sadržajima i ishodima u hrvatskim obrazovnim okvirima. Naime, učitelji razredne nastave, od kojih se očekuje da poučavaju ovaj sadržaj u sklopu nastavnog predmeta Matematika, nisu sadržaje iz vjerojatnosti iskusili kad su sami bili učenici (osim ako su išli u matematičku gimnaziju), niti su se s njima susreli tijekom svojih učiteljskih studija (niti u sklopu matematičkih kolegija, niti su radili metodiku nastave vjerojatnosti u sklopu metodičkih kolegija). Danas se ti sadržaji i aktivnosti uključuju u učiteljske studije, ali mnogi učitelji s više godina staža nemaju to iskustvo. Osim edukacija podršku učiteljima, učenicima i roditeljima u ovim novim sadržajima svakako čine udžbenici – kao autorizirani i odobreni izvori znanja za školu (Love i Pimm, 1996). Stoga su u ovom radu analizirani zadatci iz vjerojatnosti iz svih matematičkih udžbenika za razrednu nastavu, prema više različitih kriterija.

Vrste matematičkih zadataka

Udžbenici se u velikoj mjeri upotrebljavaju u osnovnoškolskoj nastavi matematike u Hrvatskoj. Pritom učitelji najviše upotrebljavaju udžbenike za pripremu nastavnog sata, a učenici za rješavanje zadataka (Glasnović Gracin i Domović, 2009). S obzirom na to da je matematički zadatak temeljni objekt na kojem počiva učenje i poučavanje matematike (Kurnik, 2000), važno je provesti analizu udžbeničkih zadataka jer zadatci otvaraju mogućnosti i kreiraju učeničke stavove prema matematici (Sullivan i sur., 2013), mogu utjecati na način kako učenici razmišljaju te ograničavati ili proširivati učeničke poglede na sadržaj koji se uči (Henningsen i Stein, 1997).

Stoga je važno analizirati udžbeničke zadatke i što oni od učenika zahtijevaju za svaku matematičku disciplinu, pa tako i za poglavlja iz vjerojatnosti. Na taj način, osim kao podrška učeniku, možemo dobiti i uvid u to koliko udžbenički sadržaj čini podršku i učiteljima, iz gore navedenih razloga. Analiza matematičkih zadataka iz udžbenika može se provesti prema različitim kriterijima, a u ovom radu donosimo neke od njih: podjelu prema aktivnosti, prema složenosti, prema vrsti odgovora te prema kontekstu (Glasnović Gracin, 2018).

Zadatci prema aktivnosti dijele se na: računanje i operiranje, prikazivanje, interpretiranje te argumentiranje i dokazivanje. Zadatci prikazivanja odnose se na zadatke u kojima učenici trebaju crtati, skicirati, konstruirati, raditi modele te brojne druge primjene u sklopu prikazivanja određenih matematičkih pojmova. Zadatci interpretiranja su zadatci u kojima učenici očitavaju i tumače ponuđene slike, tablice ili formule. Zadatci argumentiranja i dokazivanja su zadatci u kojima učenici trebaju objasniti, opisati, pokazati ili dokazati određene tvrdnje koje su tražene u zadatcima.

Zadatci prema složenosti dijele se na jednostavne zadatke, zadatke povezivanja i refleksivne zadatke. Jednostavni zadatci su zadatci gdje je potrebna samo direktna primjena naučenog sadržaja. Zadatci povezivanja predstavljaju zadatke u kojima učenici trebaju kombinirati dvije ili više aktivnosti/sadržaja kako bi riješili zadatak. Posljednja vrsta zadataka prema složenosti su refleksivni zadatci i složenija povezivanja. U takvim zadatcima učenici trebaju upotrijebiti dublje promišljanje o konačnom rješenju zadatka.

Zadatci prema vrsti odgovora se dijele na zadatke zatvorenog tipa te zadatke otvorenog tipa. Bitna razlika između ovih zadataka je u tome što se kod zadataka zatvorenog tipa naglasak stavlja na samo rješenje. Kod zadataka otvorenog tipa od učenika se očekuje da opiše, prikaže, dokaže, objasni i sl. te se često naglasak stavlja na proces dolaska do rješenja.

Zadatci prema kontekstu mogu se podijeliti u tri skupine zadataka. Prva skupina odnosi se na unutarmatematičke zadatke koji nemaju kontekst. Sljedeća vrsta zadataka prema kontekstu je realističan zadatak koji sadrži kontekst, ali kontekst imitira stvarnost izmišljenim situacijama. Posljednja vrsta zadataka prema kontekstu su autentični zadatci. Kod autentičnih zadataka kontekst koji se pojavljuje je izvorna stvarnost. Primjeri za svaku podvrstu mogu se naći u radu od Krljan (2023). Ova podjela prema aktivnosti, složenosti, vrsti odgovora te prema kontekstu bila je osnova za analizu zadataka iz vjerojatnosti u udžbenicima za razrednu nastavu.

Analiza udžbeničkih zadataka

Analizom udžbenika pokušalo se utvrditi na koji se način ishodi iz vjerojatnosti reflektiraju u matematičkim udžbenicima te koje vrste zadataka prevladavaju u matematičkim udžbenicima razredne nastave vezano za sadržaj vjerojatnosti. Istraženo je svih šest udžbeničkih kompleta za matematiku u razrednoj nastavi, odnosno poglavlja koja se odnose na vjerojatnost. Pod pojmom zadataka u ovom se radu podrazumijevala svaka uputa/pitanje koje je usmjereno učeniku i od njega očekuje odgovor. To znači da su, uz zadatke za vježbu, analizirani i motivacijski zadatci te primjeri. Poglavlja za dodatnu nastavu te uvodna i završna poglavlja nisu uzeta u obzir jer nisu ujednačena po udžbenicima.

Instrument istraživanja preuzet je od Glasnović Gracin (2018) te modificiran za potrebe ovog rada. Naime, osim vrsta matematičkih zadataka u analiziranju matematičkih udžbenika uključeni su i ishodi iz kurikuluma za vjerojatnost (MZO, 2019).

Rezultate ćemo prikazati u dva dijela. U prvom su dijelu analizirani matematički udžbenici prema ishodima iz kurikuluma, a u drugom dijelu prema vrstama zadataka. Na taj se način nastojalo dobiti jasniju sliku koje karakteristike i zahtjeve udžbenici razredne nastave učenicima i učiteljima nude iz područja vjerojatnosti.

Udžbenički zadatci prema sadržajima iz kurikuluma

Kurikulumski sadržaji s opisom domene E i ishodima iz vjerojatnosti za razrednu nastavu ukazuju na neke ključne riječi i aktivnosti (MZO, 2019), a to su: određivanje mogućeg, nemogućeg i sigurnog događaja te uspoređivanje vjerojatnosti (korištenjem pojmova vjerojatniji, manje vjerojatan i sl.). No, budući da je u opisu domene E istaknuto kako učenike treba poticati da sami provode istraživanja, opisuju događaje i ishode te donose zaključke, u okvir je, osim navedenih sadržaja, dodano i provođenje istraživanja.

S obzirom na to da su ishodi iz vjerojatnosti u razrednoj nastavi prisutni samo u 2. i 4. razredu, analizom je utvrđeno da u udžbenicima prvog i trećeg razreda nema cjelina iz vjerojatnosti. Stoga ovdje donosimo rezultate samo za 2. i 4. razred. U tablicama 2 i 3 prikazan je udio zadataka iz vjerojatnosti u ukupnom broj zadataka u pojedinom udžbeniku te broj zadataka s određenim sadržajem iz vjerojatnosti. Rezultati ukazuju na vrlo mali broj zadataka iz vjerojatnosti u odnosu na ukupan broj zadataka po pojedinom udžbeniku. U udžbeniku U2 u 2. razredu i U3 u 4. razredu zadan je samo po jedan zadatak iz vjerojatnosti.

UDŽBENIK 2. r. šifra	udio zadataka iz vjerojatnosti u uk. broju zadataka	BROJ ZADATAKA SA SADRŽAJEM IZ VJEROJATNOSTI
		moguć događaj	nemoguć događaj	uspoređivanje vjerojatnosti	siguran događaj	provođenje istraživanja
U1-2r	8/958	7	7	1	6	0
U2-2r	1/957	1	1	0	0	0
U3-2r	6/846	6	4	0	3	0
U4-2r	2/839	2	2	0	0	0
U5-2r	3/469	3	3	0	0	0
U6-2r	6/365	6	6	0	0	0

U svim udžbenicima drugog razreda pojavljuju se pojmovi moguć i nemoguć događaj u zadatcima, što je u skladu s ishodom MAT OŠ E.2.2. Udžbenici U1 i U3 uvode i određivanje sigurnog događaja. Provođenje jednostavnijih ispitivanja iz vjerojatnosti te uspoređivanje vjerojatnosti nisu prisutni u udžbenicima 2. razreda, no to i nije zadano kurikulumom za taj razred. Rezultati ukazuju da udžbenik U2 samo u jednom zadatku od učenika traži aktivnost s mogućim i nemogućim događajem, dok je kod udžbenika U4 to slučaj u dva zadatka, a u U5 u tri (tablica 2).

UDŽBENIK 4. r. šifra	udio zadataka iz vjerojatnosti u uk. broju zadataka	BROJ ZADATAKA SA SADRŽAJEM IZ VJEROJTANOSTI
		moguć događaj	nemoguć događaj	uspoređivanje vjerojatnosti	siguran događaj	provođenje istraživanja
U1-4r	11/685	7	8	4	6	2
U2-4r	7/738	2	2	6	1	0
U3-4r	1/661	0	0	1	0	0
U4-4r	3/697	3	3	2	2	0
U5-4r	13/467	9	7	8	9	0
U6-4r	9/270	3	3	6	3	0

U svim udžbenicima četvrtog razreda pojavljuje se uspoređivanje vjerojatnosti slučajnog događaja, što je u skladu s ishodom MAT OŠ E.4.2 i njegovom razradom. Provođenje istraživanja prisutno je samo u udžbeniku U1 u dvama zadatcima. Rezultati pokazuju da udžbenik U3 u cijelom svojem opsegu ima samo jedan zadatak koji se odnosi na vjerojatnost (tablica 3).

Udžbenički zadatci prema vrstama zadataka

Osim sadržajne komponente željeli smo ispitati što se u zadatcima iz vjerojatnosti od učenika traži: koje matematičke aktivnosti (treba li učenik usporediti, prikazati, interpretirati sliku ili nešto objasniti), koliko je složen zadatak (radi li se o jednostavnoj primjeni pravila ili definicije ili se pak traže povezivanja više pojmova i aktivnosti), kakav mu je odgovor (traži li se od učenik odgovor zatvorenog ili otvorenog tipa) te kakav je kontekst zadatka (je li zadatak potpuno unutarmatematički, ima li izmišljen realističan kontekst ili je autentičan iz svakodnevice).

U poglavlju Vrste matematičkih zadataka opisane su kategorije za analizu zadataka prema Glasnović Gracin (2018). U tablici 4 navedeni su elementi po kojima su se analizirali udžbenički zadatci prema vrstama te su im dodijeljene šifre.

VRSTE ZADATAKA		ŠIFRA
PREMA AKTIVNOSTI	računanje i uspoređivanje	A1
	prikazivanje	A2
	interpretiranje	A3
	argumentiranje	A4
PREMA SLOŽENOSTI	jednostavni zadatci	S1
	zadatci povezivanja	S2
	refleksija i složenija povezivanja	S3
PREMA VRSTI ODGOVORA	zatvorenog tipa	O1
	otvorenog tipa	O2
PREMA KONTEKSTU	unutarmatematički zadatci	K1
	realistični zadatci	K2
	autentični zadatci	K3

Rezultati analize udžbenika prema vrstama zadataka prikazani su u tablicama 5 i 6.

UDŽBENIK 2. r. šifra	udio zadataka iz vjerojatnosti u uk. broju zadataka	BROJ ZADATAKA IZ VJEROJATNOSTI PREMA VRSTAMA ZADATAKA
		A1	A2	A3	A4	S1	S2	S3	O1	O2	K1	K2	K3
U1-2r	8/958	0	1	4	6	5	3	0	4	4	0	6	2
U2-2r	1/957	1	1	1	0	0	1	0	1	0	0	0	1
U3-2r	6/846	3	0	2	5	3	3	0	0	6	1	5	0
U4-2r	2/839	1	0	1	2	1	1	0	0	2	0	2	0
U5-2r	3/469	0	0	0	3	3	0	0	0	3	0	2	1
U6-2r	6/365	1	1	3	1	4	2	0	5	1	0	6	0

Rezultati za 2. razred ukazuju na interpretiranje (tumačenje slike) i objašnjavanje kao dominantne aktivnosti u zadatcima vezanima za vjerojatnost razredne nastave (tablica 5). Analizirani zadatci najčešće se odnose na jednostavne zadatke ili zadatke povezivanja, i to s realističnim kontekstom. Udžbenici U1, U3, U4 i U5 u većini analiziranih zadataka zahtijevaju objašnjavanje ili argumentiranje situacija iz vjerojatnosti, što su svakako poželjne matematičke aktivnosti za bolje usvajanje novih pojmova. Niti jedan udžbenik 2. razreda ne sadrži zadatak s refleksijom i složenijim povezivanjima. Ovaj nalaz može biti u skladu s osnovnim zahtjevima iz kurikuluma za 2. razred. Rezultati također ukazuju na različitost među udžbenicima vezano za vrstu odgovora: udžbenik U6 ima većinu zadataka koji traže odgovor zatvorenog tipa, udžbenici U3, U4 i U5 imaju sve zadatke iz vjerojatnosti otvorenog tipa, dok udžbenik U1 nudi jednak broj otvorenih iz zatvorenih zadataka (tablica 5).

UDŽBENIK 4. r. šifra	udio zadataka iz vjerojatnosti u uk. broju zadataka	BROJ ZADATAKA IZ VJEROJATNOSTI PREMA VRSTAMA ZADATAKA
		A1	A2	A3	A4	S1	S2	S3	O1	O2	K1	K2	K3
U1-4r	11/685	2	0	2	10	8	3	0	0	11	0	6	5
U2-4r	7/738	5	0	0	5	4	3	0	2	5	1	6	0
U3-4r	1/661	1	0	1	1	0	1	0	0	1	0	0	1
U4-4r	3/697	0	0	0	3	3	0	0	1	2	0	2	1
U5-4r	13/467	0	0	7	7	11	2	0	8	5	0	11	2
U6-4r	9/270	1	4	2	9	4	4	1	1	8	1	7	1

Rezultati za 4. razred ukazuju na dominaciju zadataka argumentiranja među analiziranim zadatcima. Ovaj nalaz povezan je i s većinom zadataka otvorenog tipa iz vjerojatnosti. To znači da, iako je zadataka malo, u njima se od učenika većinom traži argumentiranje zašto je neki događaj vjerojatniji od drugoga. Udžbenik U6 zahtijeva i prikazivanje, što nije slučaj u ostalim udžbenicima. Udžbenik U2 u svim analiziranim zadatcima zahtijeva računanje, a radi se o računskim zadatcima u kojima je zadano i pitanje iz vjerojatnosti vezano za račun. Kao i u drugom razredu, ispitani zadatci iz svih šest udžbenika najčešće se odnose na jednostavne zadatke ili zadatke povezivanja, i to s realističnim kontekstom.

Unatoč malom broju zadataka za analizu možemo zaključiti da se u četvrtom razredu od učenika više traži argumentiranje o pojmovima iz vjerojatnosti u odnosu na drugi razred, što može biti u skladu s dobi i predznanjem učenika. Iako je broj zadataka iz vjerojatnosti povećan u 4. razredu u odnosu na drugi u gotovo svim udžbenicima, rezultati ukazuju na (pre)mali broj zadataka sa sadržajem iz vjerojatnosti, posebice u nekim udžbeničkim kompletima. To upućuje da će učitelji razredne nastave trebati sami sastaviti još zadataka kada poučavaju sadržaje vjerojatnosti ili će trebati posegnuti za drugim izvorima.

Zaključak

Rezultati ukazuju na postavljanje pitanja jesu li udžbenici iz matematike za razrednu nastavu, posebice oni s minimalnim brojem zadataka, uistinu podrška učenicima i učiteljima u učenju i poučavanju sadržaja iz vjerojatnosti. Možemo pretpostaviti da je mali broj zadataka posljedica i malog broja ishoda iz vjerojatnosti u razrednoj nastavi. No, neki udžbenici nisu svojim zadatcima pokrili ni te ishode, iako je nakon reforme svaki udžbenik prolazio recenziju Ministarstva znanosti i obrazovanja. Bitno je ipak napomenuti i kako nije struktura svakog udžbenika jednaka jer uz udžbenike postoje i metodički priručnici, radne bilježnice te zbirke zadataka u kojima se mogu nalaziti vrste zadataka koje nisu prisutne u udžbenicima. No, Zakon o udžbenicima i drugim obrazovnim materijalima za osnovnu i srednju školu (2018) ističe da udžbenik „služi kao cjelovit izvor za ostvarivanje svih odgojno-obrazovnih ishoda“ (čl. 3) te da „sadržaj i struktura udžbenika mora omogućavati učenicima samostalno učenje i stjecanje različitih razina i vrsta kompetencija, kao i vrednovanje usvojenosti odgojno-obrazovnih ishoda i očekivanja međupredmetnih tema“ (čl. 3). Stoga možemo zaključiti da u području poučavanja vjerojatnosti postoji još mnogo izazova i prostora za poboljšanja, a učiteljima (i učenicima i roditeljima) svakako treba podrška u ovom području. I to ne samo odgovarajućim udžbenicima, već i sustavnim edukacijama za učitelje, tematskim skupovima s ciljanom temom iz poučavanja vjerojatnosti (ili čak cijele domene E) kojima će učitelji razredne nastave iskusiti vjerojatnost različitim pokusima, na kojima će dobiti i širu izobrazbu iz područja vjerojatnosti, ali i što raditi na dodatnoj nastavi iz vjerojatnosti, kako oplemeniti dopunsku nastavu sadržajima iz vjerojatnosti i sl. Vjerojatnost se smatra mlađom granom matematike i nije opterećena velikom i tromom tradicijom klasičnog poučavanja poput nekih drugih grana školske matematike. Stoga su pokusi, iskustveno učenje i istraživanja vrlo lako ušli u učionice diljem svijeta. Igrolikim će aktivnostima učenici razvijati svoj interes prema matematici te će usvajati jezik vjerojatnosti, ali i otkrivati sam koncept vjerojatnosti (Soucie, 2011). No, za to je potreban kompetentan učitelj, ali i materijalna sredstva poput udžbenika koji će im biti podrška jer, kako je rečeno ranije, udžbenički zadatci su u većini razreda najčešći objekti kojima se uči matematički sadržaj i dobiva slika o tome što matematika jest.

Primjeri aktivnosti

Na kraju, donosimo nekoliko aktivnosti koje nisu prisutne u udžbenicima, a mogu biti podrška učenicima i učiteljima za kvalitetniju nastavu vjerojatnosti. Istraživanje je pokazalo da u udžbenicima nedostaju neki tipovi aktivnosti, poput prikazivanja situacija, vježbanja procjene te manjih istraživanja i refleksije. Primjeri koji slijede odnose se upravo na te ideje. Cilj je učitelje potaknuti da sami osmisle svoje zadatke te da na ovim primjerima uvide kako se sadržaj vjerojatnosti može uvoditi na razne načine.

1. primjer: Prikazivanje crtanjem

Zamisli da bez gledanja izvlačiš kuglice iz kutije.

(Napomena: zadatci su namijenjeni za 2. i 4. razred, ali potpitanja zadataka mogu se prilagođavati ovisno o razredu i ishodima.)

1. Nacrtaj situaciju u kojoj je moguće izvući plavu kuglicu. Zatim nacrtaj još tri slike situacija u kojima je moguće izvući plavu kuglicu, ali da se situacije matematički razlikuju. Po čemu se slike razlikuju? Što sve možeš mijenjati na crtežu, ali tako da uvijek bude moguće izvući plavu kuglicu? Što mora ostati isto?
2. Nacrtaj situaciju u kojoj je nemoguće izvući zelenu kuglicu. Zatim nacrtaj još tri slike situacija u kojima je nemoguće izvući zelenu kuglicu, ali da se situacije razlikuju. Po čemu se slike razlikuju? Što sve možeš mijenjati na crtežu, ali tako da uvijek bude nemoguće izvući zelenu kuglicu? Što mora ostati isto?
3. Nacrtaj situaciju u kojoj ćeš sigurno izvući crvenu kuglicu. Zatim nacrtaj još tri slike situacija u kojima ćeš sigurno izvući crvenu kuglicu, ali da se situacije razlikuju. Po čemu se slike razlikuju? Što sve možeš mijenjati na crtežu, ali tako da uvijek bude sigurno da ćeš izvući crvenu kuglicu? Što mora ostati isto?
4. Nacrtaj dvije slike situacija tako da na svakoj bude vjerojatnije da se izvuče bijela nego crna kuglica. Objasni na što trebaš paziti, a što se može mijenjati.
5. Nacrtaj sliku situacije tako da bude najmanje vjerojatno da se iz kutije izvuče crvena kuglica, najviše vjerojatno da se izvuče zelena, ali da bude moguće izvući i bijelu i crnu kuglicu. Zatim nacrtaj još jedan primjer za koji vrijede uvjeti iz prethodne rečenice. Objasni na što trebaš paziti, a što se može mijenjati. Koja je razlika, a koja sličnost između vjerojatno i najmanje vjerojatno?
6. Od nacrtanih slika iz ovog zadatka napravi plakat ili strip s različitim mogućnostima. Ispod slika stavi objašnjenja ili zadatke za čitatelje.

2. primjer: Vježbanje procjene

U 2. razredu učenici poznaju brojeve do 100 pa je korisno povezati procjenu količine s procjenom vjerojatnosti slučajnog događaja. Slično se može raditi i u 4. razredu s većim brojevima.

1. Pogledaj slike pa za svaku procijeni koliko je bijelih, a koliko crvenih kuglica. Je li vjerojatnije da na pojedinoj slici bez gledanja izvučeš bijelu ili crvenu kuglicu? Objasni.

2. Oboji kuglice tako da je na svakoj slici jednako vjerojatno izvući bijelu ili plavu kuglicu. Objasni zašto.

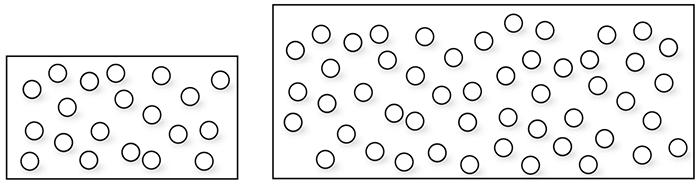
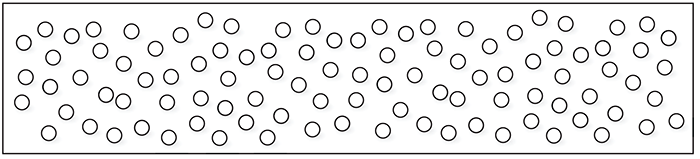
U ovom zadatku moguće je preinačiti sliku mijenjajući broj kuglica na slici. Možemo početi sa slikama 20 kuglica, zatim stavljamo razne slike s 50 kuglica, a na kraju i sa 100 kuglica.

3. primjer: Istraživanje

Vlastito iskustvo ponavljanja slučajnih pokusa veoma je važna baza za kasnije računanje vjerojatnosti. Zakon velikih brojeva nam govori o tome da ako neovisno i pod jednakim uvjetima veliki broj puta ponavljamo neki slučajan pokus, relativna frekvencija događaja bit će približno jednaka vjerojatnosti tog događaja. Pogodni primjeri za to su bacanje novčića, bacanje igraće kocke, izvlačenje kuglica ili karata bez gledanja, kolo sreće i sl. Učenici u razrednoj nastavi neće računati vjerojatnost, ali će promatrati kako se s većim brojem ponavljanja pokusa polako izjednačavaju brojevi različitih nezavisnih događaja.

1. Prije bacanja kocke: Što misliš, pojavljuje li se bacanjem igraće kocke neki broj češće od drugih? Što misliš, je li vjerojatnije da ćeš dobiti 6 ili 3? Što misliš, je li vjerojatnije da ćeš dobiti 1 ili 5? Objasni zašto tako misliš.
   Aktivnosti: (i) Bacaj igraću kocku 30 puta zaredom i bilježi koliko je puta pao koji broj. Možeš uključiti i svoje ukućane u aktivnost. Možeš li donijeti neke zaključke iz rezultata? Usporedi svoje rezultate s ostalim prijateljima u razredu.
   (ii) Zatim u razredu zbrojite sva pojavljivanja po pojedinom broju, tj. pronađite ukupan broj pojavljivanja broja 1, broja 2 itd. za vaš razred. Što primjećuješ? Razlikuju li se zaključci u odnosu na tvoje ranije zaključke i razmišljanja?
   (iii) Zatim u cijeloj generaciji učenika tvoje škole (npr. 4.a, 4.b i 4.c) zbrojite sva pojavljivanja po pojedinom broju, tj. pronađite ukupan broj pojavljivanja broja 1, broja 2 itd. za sve četvrte razrede.
   Diskusija: Što primjećuješ? Razlikuju li se zaključci u odnosu na tvoje ranije zaključke i razmišljanja?
2. Može se organizirati slična aktivnost kao pod a), ali s bacanjem novčića (pismo/glava), izvlačenjem kuglica, karata ili okretanjem kola sreće.
3. Početna aktivnost: Učenici bacaju dvije igraće kocke i zbrajaju dobivene brojeve. Raspravljaju o tome koje je zbrojeve nemoguće dobiti, a koje je zbrojeve moguće dobiti.
   Igra: Zatim igraju igru s pijunima i pločom u kojoj svaki učenik odabire jedan broj (mogu odabrati i jednake brojeve). Učenik čiji je odabrani broj jednak zbroju brojeva na kockicama pomiče se za jedno mjesto na ploči. Pobjednik je onaj učenik koji prvi dođe do cilja.
   Diskusija: Provodi se diskusija o tome je li svaki zbroj od 2 do 12 jednako vjerojatan (da će pasti) ili su neki zbrojevi više/manje vjerojatniji od drugih. Učenici obrazlažu svoja mišljenja.
   Istraživanje: Poput aktivnosti iz Primjera 4 učenici bacaju par kocaka mnogo puta i uvjeravaju se koji su ishodi najpovoljniji za pobjedu u igri. Bacanje para kocaka može se opet odvijati na razini razreda ili cijele generacije učenika. Važno je da se par kocaka baci zaista mnogo puta.
   
   

4. primjer: Promišljanje i analiza

Za učenike u razrednoj nastavi koji mogu i žele više, poželjno je napraviti i korak dalje te prikazati primjere aktivnosti s uvjetnom vjerojatnosti, uz poticanje procjene i promišljanja.

1. Zamisli da u kutiji imaš tri kuglice kao na slici. Što je vjerojatnije, koju ćeš izvući?

Zamisli da izvučeš jednu kuglicu, a kada ju izvučeš, ne vraćaš ju natrag u kutiju, već ti ostanu dvije. Što je sada vjerojatnije, koju ćeš izvući? To naravno ovisi o tome koja je kuglica izvučena prva. Pogledajmo sljedeću sliku mogućnosti izvlačenja kuglica:

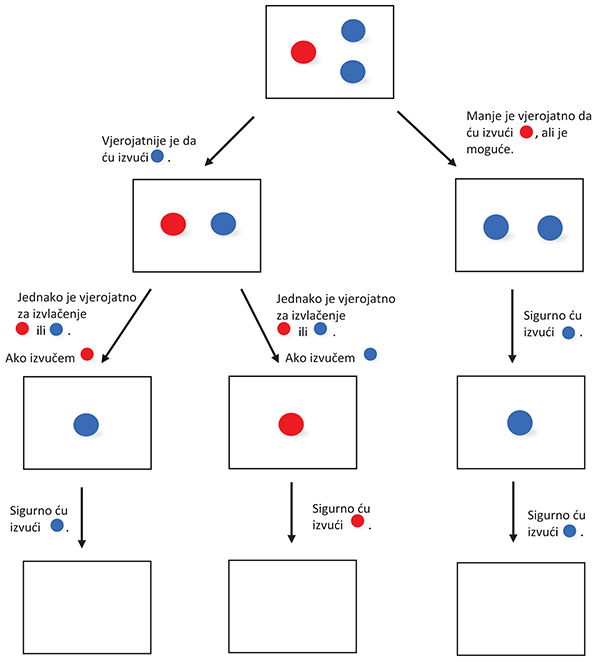
Opiši ovu sliku uz vježbanje pojmova vjerojatno, vjerojatnije, sigurno i sl.

Oboji put više vjerojatnijih događaja, od početka do prazne kutije. U slučaju da je negdje jednako vjerojatno, oboji oba puta.

2. Pogledaj sljedeće slike i na isti način kao u a) zadatku nacrtaj sve mogućnosti kako doći do prazne kutije uz izvlačenje jedne po jedne kuglice bez vraćanja – za svaku zadanu sliku. Zatim daj prijatelju da opiše sliku.

(i)                                     (ii)                                     (iii)                                    (iv)

Literatura

1. Glasnović Gracin D. (2018): Requirements in mathematics textbooks: a five-dimensional analysis of textbook exercises and examples, International Journal of Mathematical Education in Science and Technology, 49(7), 1003–1024.
2. Glasnović Gracin, D. i Domović, V. (2009). Upotreba matematičkih udžbenika u nastavi viših razreda osnovne škole. Odgojne znanosti, 11, 297–317.
3. Henningsen, M. i Stein, M. (1997). Mathematical tasks and student’s cognition: Classroom-based factors that support and inhibit high-level mathematical thinking and reasoning. Journal for Research in Mathematics Education, 28(5), 524–549.
4. Huzak, M. (2005). Vjerojatnost u osnovnoj školi. Poučak – časopis za metodiku i nastavu matematike, 6(23), 36–38.
5. Krljan, I. (2023). Sadržaj statistike i vjerojatnosti u matematičkim udžbenicima u primarnom obrazovanju, Diplomski rad, Sveučilište u Zagrebu, Učiteljski fakultet.
6. Kurnik, Z. (2000). Matematički zadatak. Matematika i škola, 7, 51–58.
7. Love, E. i Pimm, D. (1996).“This is so”: a text on texts. In A. J. Bishop, K. Clements, C. Keitel, J. Kilpatrick i C. Laborde (Eds.), International handbook of mathematics education, Vol. 1. (pp. 371–409). Dordrecht: Kluwer.
8. Ministarstvo znanosti i obrazovanja (2019). Kurikulum nastavnog predmeta Matematika za osnovne škole i gimnazije. Zagreb.
9. Loparić, S. (2019). Vjerojatnost i statistika – zašto, kada, kako?. Poučak – časopis za metodiku i nastavu matematike, 20(80), 45–51.
10. Polaki, M. V. (2002.). Using instruction to identify key features of basotho elementary students’ growth in probabilistic thinking. Mathematical Thinking and Learning, 4(4), 285–313.
11. Soucie, T. (2011). Vjerojatnost u nižim razredima osnovne škole. Poučak – časopis za metodiku i nastavu matematike, 12(47), 34–43.
12. Sullivan, P., Clarke, D. M. i Clarke, B. A. (2013). Teaching with tasks for effective mathematics learning. Springer.
13. Zakon o udžbenicima i drugim obrazovnim materijalima za osnovnu i srednju školu (NN 116/2018-2288).
    https://narodne-novine.nn.hr/clanci/sluzbeni/2018_12_116_2288.html

---