Matematički sadržaji izgrađuju se na dva načina: vertikalno, povećavajući njihovu složenost, i horizontalno, okupljajući više pojmova i procedura u jedan novi objekt. Konkretne aktivnosti s matematičkim sadržajima na nižim razinama obrazovanja olakšavaju razumijevanje i primjenu apstraktnih matematičkih ideja na višim razinama obrazovanja. Obratno, rutinski matematički sadržaji viših razina obrazovanja predmet su problemskih i istraživačkih aktivnosti na nižim razinama obrazovanja.
U ovom radu dani su teorijski sadržaji koji podržavaju vertikalnu korelaciju i konkretni primjeri kako ju ostvariti na različitim razinama matematičkog obrazovanja.
1. Uvod
Obrazovanje budućih učitelja podrazumijeva obrađivanje matematičkih sadržaja iznad obrazovne razine u kojoj će podučavati. Time se njihova znanja i kompetencije produbljuju kako bi im rad bio utemeljen i usklađen s matematikom viših razina obrazovanja, počevši od razredne nastave matematike, preko osnovnoškolskog i srednjoškolskog do sveučilišnoga matematičkog obrazovanja. Budući učitelji obrazuju se tako da mogu ostvariti vertikalnu korelaciju u nastavi matematike, na razini na kojoj poučavaju i u suradnji s nastavnicima viših obrazovnih razina.
Korelacija jest isticanje i interpretiranje odnosa između različitih sadržaja za koje se može utvrditi poveznica. Korelacije mogu biti različite vrste. Ovisno o podrijetlu sadržaja korelacija može biti unutarpredmetna i međupredmetna. Iako se izrijekom ne spominje, u kurikulumu nastavnog predmeta matematika nalaze se sljedeće asocijacije na korelaciju [7]:
- Poučavanje matematike tijekom školovanja je strukturirano, pa se velika pozornost posvećuje postupnosti u prihvaćanju i usvajanju matematičkih znanja te uspostavljanju veza među njima. (str. 7.)
- Matematičke se kompetencije neprestano razvijaju putem uravnoteženog preplitanja matematičkih procesa i domena predmeta matematika, ali i putem drugih područja odgoja i obrazovanja te tijekom svih faza školovanja. (str. 8.)
- Dobro i pravodobno usvojeni matematički koncepti potiču razumijevanje i snalaženje u različitim područjima kurikuluma. Isto tako, mnogi koncepti usvojeni u drugim područjima i drukčijim pristupom obogaćuju učenje i poučavanje u predmetu Matematika. Takvim načinom, stalnim korelacijama i integracijom unutar kurikuluma tijekom cijeloga školovanja učenici matematiku prihvaćaju kao dio okružja, a matematičke kompetencije primjenjuju u različitim aspektima učenja i života. (str. 8.)
- Domene se postupno razvijaju i nadograđuju cijelom vertikalom učenja i poučavanja matematike. (str. 12.)
- Planiranjem i povezivanjem matematike s drugim područjima kurikuluma, međupredmetnim temama i sadržajima ostalih predmeta te njihovom cjelovitom primjenom u profesionalnoj i privatnoj sferi života učenje i poučavanje matematike u potpunosti zaokružuje svoju svrhu. (str. 233.)
- Povezivanje podrazumijeva uspostavljanje veza među različitim matematičkim konceptima, između matematike i drugih područja učenja, kao i povezivanje matematike i svakodnevnoga života (str. 235.)
Zelenom bojom istaknute su asocijacije na unutarpredmetnu korelaciju – povezivanje sadržaja iz različitih područja matematike, odnosno domena i procesa kurikuluma predmeta matematika. Plavom bojom istaknute su asocijacije na međupredmetnu korelaciju – povezivanje matematičkih sadržaja sa sadržajima iz drugih područja, odnosno drugih predmeta i međupredmetnih tema. Ovisno o redoslijedu poučavanja sadržaja unutarpredmetna korelacija može biti horizontalna, ako se povezuju sadržaji predviđeni za istu obrazovnu razinu ili vertikalna, ako se povezuju sadržaji previđeni za različite obrazovne razine. Vertikalna povezanost je manje naglašena u kurikulumu i izravno se spominje rečenicom koja je gore istaknuta crvenom bojom.
Struktura matematike kao nastavnog predmeta takva je da sadržaji moraju biti posloženi određenim redoslijedom. Time se podrazumijeva da kurikulum poštuje vertikalnu osovinu sadržaja, ali ne propisuje kako ostvariti njihovu povezanost. Odgovornost je nastavnika stvoriti prilike u nastavi matematike za uspostavljenje vertikalnih poveznica između matematičkih sadržaja jednako kao poveznica ostalih vrsta. U konačnici je poželjno da učenik uspostavi veze između sadržaja unutar i izvan matematike i po vertikali matematičkog obrazovanja jer time jača svoje matematičko znanje.
U daljnjem tekstu opisat će se pojmovi iz edukacijske matematike povezani s vertikalnom korelacijom i dati primjeri aktivnosti koji podržavaju vertikalnu povezanost matematičkih sadržaja.
2. Vertikalna matematizacija
Jedan od najznačajnijih doprinositelja metodici matematike bio je Hans Freudenthal, nizozemski matematičar koji je djelovao u drugoj polovici 20. stoljeća u primijenjenoj matematici, geometriji i topologiji. Zalagao se za poučavanje matematike kakva je relevantna za učenike i vođeno otkrivanje u nastavi matematike te radio na projektu realističnog matematičkog obrazovanja. Smatrao je kako učenici ne trebaju biti primatelji gotovih matematičkih sadržaja, nego samostalno razvijati matematičke ideje radeći na zadanim problemima. To je takozvani proces matematizacije i razlikuju se dvije vrste [8]. Horizontalna matematizacija odnosi se na korištenje matematičkih alata za rješavanje problema realnog konteksta, odnosno uspostavljanje veze između realnog svijeta i apstraktnih matematičkih sadržaja. Vertikalna matematizacija odnosi se na reorganizaciju unutar matematike povezivanjem koncepata i strategija, odnosno razvijanje matematičkih sadržaja po složenosti.
2.1. Kutija maksimalnog obujma
Prvi primjer je aktivnost koja je predložena za učenike viših razreda osnovne škole [3] i zadatak u udžbenicima za četvrti razred srednje škole [2]. Učenicima se zadaje problem sljedećeg oblika:
Primjer 1. Od predloška oblika kvadrata treba izraditi otvorenu kutiju oblika kvadra koja je najvećeg obujma.
Proveli smo primjerenu aktivnost s učenicima četvrtog razreda osnovne škole. Oni su radili s konkretnim materijalom (slika 1), određivali su obujam kvadra izrađenog od predloška oblika kvadrata prebrojavanjem jediničnih kocaka, organizirali podatke tako da su sustavno ispisali moguće ishode i uspoređivali rezultate kako bi odredili rješenje. Učenici su radili timski, svaki je učenik izradio kutiju drukčijih dimenzija i odredio njezin obujam te su objedinili podatke u jednu tablicu. Stupci tablice sadrže podatke o duljini stranice izrezanog kvadrata na rubu predloška, duljini, širini i visini kutije te izračunatom obujmu kutije. Za predložak duljine 12 cm kutija nastala izrezivanjem kvadrata stranice duljine 2 cm na rubu predloška, dimenzija 8 cm x 8 cm x 2 cm ima obujam 128 cm3 koji je najveći za dani predložak.
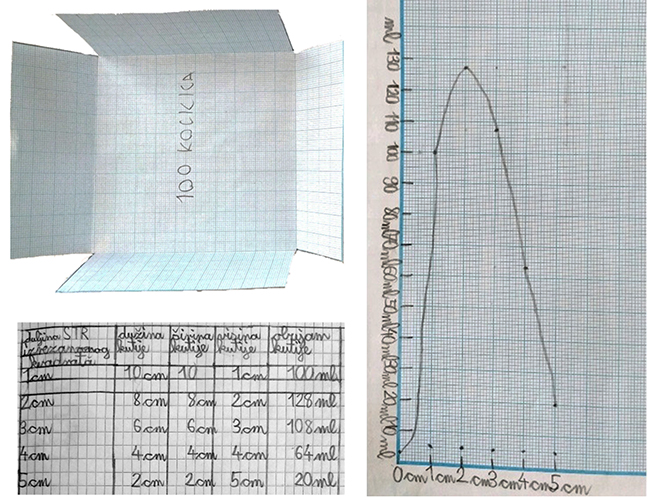
Učenici viših razreda osnovne škole upotrebljavaju apstraktnije, njima primjerene načine prikazivanja i komunikacije u istoj aktivnosti. Ako duljina stranice predloška oblika kvadrata iznosi $a$, onda izrezivanjem kvadrata stranice duljine $x$ na rubovima predloška dobije se kutija oblika kvadra kojemu je osnovka kvadrat stranice duljine $a-2x$, a visina $x$. Učenici će obujam kutije iskazati algebarskim izrazom $V=(a-2x)^2\cdot x$ te izračunavanjem vrijednosti otkrivati kutiju najvećeg obujma. Odnos između visine i obujma kutije se može prikazati grafički, kako je prikazano za predložak duljine 12 cm (slika 1). Iz algebarskog ili grafičkog prikaza učenici mogu određivati kolika treba biti duljina stranice kvadrata koji se izreže na rubovima predloška kako bi se dobila kutija određenog obujma i obratno koliki će biti obujam kutije, ako se izreže kvadrat određene duljine stranice na rubovima predloška. Pri tom mjerni brojevi ne moraju biti prirodni brojevi. Učenici mogu primijetiti da za zadani obujam mogu izraditi dvije različite kutije različitih dimenzija osim za slučaj kutije najvećeg obujma.
Za učenike srednje škole ovo je zadatak koji se rutinski rješava primjenom diferencijalnog računa. Obujam kutije opisuje se polinomom trećeg stupnja $V(x)=4x^3-4ax^2+a^2x$, pri čemu je nezavisna varijabla $x$ duljina stranice kvadrata izrezanog u rubu predloška odnosno visina kutija i manja od polovine duljine predloška, $x\in\left\langle0,\frac{a}{2}\right\rangle$. Istraživanjem derivacije i stacionarnih točaka utvrdi se kako funkcija postiže maksimum vrijednosti $\frac{2a^3}{27}$ kad je nezavisna varijabla, odnosno visina kutije ili duljina stranice izrezanog kvadrata jednaka je šestini duljine predloška.
| Domene: Brojevi, Algebra i funkcije, Oblik i prostor, Mjerenje (i Podatci, statistika i vjerojatnost) Procesi: Prikazivanje i komunikacija, Povezivanje, Rješavanje problema i matematičko modeliranje, Primjena tehnologije Aktivnosti: Iz predloška oblika kvadrata zadanih dimenzija treba odrediti otvorenu kutiju oblika kvadra koja je najvećeg obujma. |
3. Pitagorin poučak
Pravilnosti u geometriji izvrsna su podloga za učenička matematička otkrića. U razrednoj nastavi matematike učenici konstruiraju likove po zadanom pravilu, promatraju obilježja i iskazuju primjerenim rječnikom pravilnosti poput nejednakosti trokuta, zbroja kutova u trokutu, Talesova poučka o obodnom kutu nad promjerom kružnice i Pitagorina poučka. Učenici četvrtog razreda osnovne škole su zajednički rješavali zadatak [6]:
Primjer 2. Opseg trokuta je 24 dm. Konstruiraj takve trokute. Kojoj vrsti trokuta pripada svaki trokut? Konstruiraj kvadrate nad stranicama trokuta i izračunaj njihove površine. U kakvom su odnosu površine kvadrata nad stranicama trokuta?
Sadržaji razredne nastave uključuju vrste kutova, vrste trokuta s obzirom na duljine stranica, pravokutan trokut, konstrukciju i opseg trokuta, konstrukciju i površinu kvadrata, ali se ne obrađuju vrste trokuta s obzirom na mjeru kutova. Kada učitelji vode učenike, oni uspješno razlikuju vrste trokuta prema mjeri kutova. Kako učenici razredne nastave ne obrađuju decimalne brojeve, očekivalo se da će navesti trokute kojima su duljine stranica iskazane u decimetrima prirodni brojevi. U suprotnom uvjet treba naglasiti u zadatku.
Na dvorištu je provedena istraživačka aktivnost u dva dijela. Pritom su se učenici koristili kredama i geometrijskim priborom za ploču. Prvo su učenici određivali duljine stranica trokuta kojima je opseg 24 dm. U ovom dijelu učenici osvijeste nejednakost trokuta kao pravilnost u geometriji kada primijete kako trebaju biti pažljivi pri odabiru duljina stranica trokuta. Ako je jedna odabrana stranica predugačka, druge dvije stranice će se poklopiti i neće se moći konstruirati trokut. U otvorenim zadatcima u kojima je potrebno navesti sva rješenja, učenike se potiče da budu sustavni i organizirani pri ispisivanju i prikazivanju mogućih ishoda. Kad su pronašli sve mogućnosti, učenici su konstruirali dobivene trokute i prepoznali kojoj vrsti pripada pojedini trokut s obzirom na duljinu stranica i vrstu kutova.
U drugom dijelu aktivnosti učenici su konstruirali kvadrate nad stranicama trokuta i izračunali površine tih kvadrata. Promatrali su, razgovarali, uspoređivali površine, vrste trokuta, kako bi otkrili pravilnost. Naglasak je bio na otkrivanju Pitagorina poučka. U slučaju jednakosti izračunatih površina, učenici su zaključili da je dobiveni trokut pravokutan. Tijekom aktivnosti učenici su primjenjivali rutinske procedure – konstrukciju trokuta, konstrukciju kvadrata i izračunavanje površine kvadrata, povezivali pojmove – opseg trokuta, vrste kutova, vrste trokuta te rasuđivali, komunicirali o rezultatima kako bi došli do heureke (slika 2).

Učenici viših razreda osnovne škole isti zadatak rješavaju prikazujući i komunicirajući rezultate primjerenim matematičkim jezikom (tablica 1). Istražujući trokute opsega 24 cm, zbroj površina kvadrata nad kraćim stranicama, površinu kvadrata nad najduljom stranicom trokuta i vrstu rezultirajućeg trokuta, učenici će doći do obrata Pitagorina poučka:
Neka su $a$, $b$ i $c$ stranice trokuta i $c$ najdulja medu njima. Ako vrijedi $a^2+b^2=c^2$ trokut je pravokutan.
| $a$ | $b$ | $c$ | $a^2+b^2$ | $c^2$ | vrsta trokuta |
| $2$ | $11$ | $11$ | $125$ | $121$ | šiljastokutan |
| $3$ | $10$ | $11$ | $109$ | $121$ | tupokutan |
| $\ldots$ | |||||
| $4$ | $10$ | $10$ | $116$ | $100$ | šiljastokutan |
| $5$ | $9$ | $10$ | $106$ | $100$ | šiljastokutan |
| $6$ | $8$ | $10$ | $100$ | $100$ | pravokutan |
| $7$ | $7$ | $10$ | $98$ | $100$ | tupokutan |
| $\ldots$ | |||||
Tablica 1. Trokuti opsega 24 cm, duljine stranica, površine kvadrata nad stranicama i vrste tih trokuta
U primjeru 2 za opseg trokuta odabran je takav opseg za koji je jedan od dobivenih trokuta s cjelobrojnim duljinama stranica pravokutan. Promatrajući rezultate u tablici 1, može se uočiti generalizacija Pitagorina poučka i njegova obrata. Odnos između vrijednosti $a^2+b^2$ i $c^2$ općenito je povezan s vrstom trokuta s obzirom na mjeru kutova, a ne samo u slučaju pravokutnog trokuta.
Neka su $a$, $b$ i $c$ stranice trokuta i $c$ najdulja među njima.
- Ako je $c^2>a^2+b^2$, trokut je tupokutan.
- Ako je $c^2=a^2+b^2$, trokut je pravokutan.
- Ako je $c^2<a^2+b^2$, trokut je šiljastokutan.
Obrat Pitagorina poučka treba posebno osvijestiti i primjenjivati, kao u sljedećem primjeru:
Primjer 3. Konstruirajte trokut $ABC$ ako su zadane duljine stranica $a=5$ cm i $c=6$ cm i težišnica $t_c=4$ cm na stranicu $c$. Kojoj vrsti trokuta pripada trokut $ABC$?
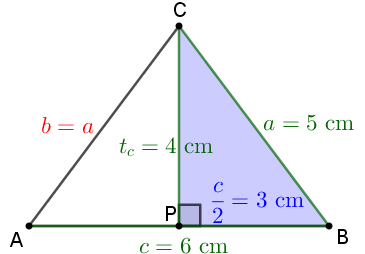
Pri analizi konstruktivnog zadatka uoči se trokut kojemu su stranice duljine 3 cm, to je polovina stranice $c$, 4 cm i 5 cm (slika 3). Koristeći se obratom Pitagorina poučka, utvrdi se kako je taj trokut pravokutan. Tada je dana težišnica ujedno i visina trokuta pa je trokut jednakokračan i konstrukcija se značajno pojednostavni.
Prethodne aktivnosti su predradnje za razumijevanje konteksta poučka o kosinusu, što je sadržaj na razini srednjoškolskog obrazovanja:
Neka su $a$, $b$ i $c$ stranice trokuta, $c$ najdulja među njima i $\gamma$ kut nasuprot stranici $c$. Vrijedi \begin{equation}c^2=a^2+b^2-2ab\cos\gamma. \tag1\label{KP}\end{equation}
Poučak o kosinusu jest generalizacija Pitagorina poučka [5]. Iz odnosa danog u (1) slijede odnosi koji su istraživani u prethodno opisanim aktivnostima.
| Domene: Oblik i prostor, Mjerenja Procesi: Prikazivanje i komunikacija, Logičko mišljenje, argumentiranje i zaključivanje Aktivnosti: Istražiti kako duljine stranica trokuta određuju vrstu trokuta s obzirom na mjeru unutrašnjih kutova. |
4. Didaktička transpozicija
Antropološka teorija didaktike je teorijski okvir koji je razvio francuski matematičar Yves Chevallard primarno za metodiku matematike, ali se primjenjuje i u drugim znanostima koje u fokusu imaju znanje. ATD kaže da znanje nije jednoznačno određeno, nego njegov oblik ovisi o instituciji u kojoj se upotrebljava[1]. To znači da neki objekt znanja nastaje u jednoj instituciji i kada prelazi u drugu instituciju mijenja se, transponira kako bi bolje odgovarao novim okolnostima. Posebno to vrijedi i za obrazovanje gdje se upotrebljava pojam didaktička transpozicija, kao transpozicija, promjena znanja u kontekstu obrazovanja (slika 4).
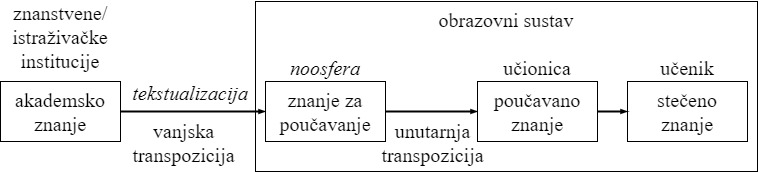
Pri didaktičkoj transpoziciji jedan objekt znanja prolazi više promjena. Izvorni oblik je akademsko znanje koje je nastalo u znanstvenim ili istraživačkim institucijama izvan obrazovnog sustava. Odgovorne osobe i institucije biraju i formuliraju koje znanje je primjereno za poučavanje. Tako nastaju kurikulum, metodički priručnici, udžbenici i drugi dokumenti. U drugom koraku učitelj tumači to propisano znanje i kreira poučavano znanje u učionici. Tek u trećem koraku transpozicije izvornog znanja učenik stječe znanje. Može se reći kako je cilj matematičkog obrazovanja da stečeno znanje učenika bude usklađeno s akademskim znanjem. No pri transponiranju znanja često se zaboravi kako je ono nastalo, otkuda je došlo, koja je njegova svrha, čemu služi ili kako se učenici pitaju „Što će to meni u životu?“.
U ATD-u povlači se razlika između dviju vrsta kurikuluma. Kurikulum po kojemu se znanje poučava radi sebe samoga i predviđeno je obraditi niz sadržaja, a naziva se Posjećivanje spomenika jer kad dođe red na novi objekt znanja svladamo ga, divimo mu se i prelazimo na sljedeći objekt znanja. Druga vrsta kurikuluma polazi od jednog pitanja te se tražeći odgovor na to pitanje otkrivaju nova znanja i postavljaju nova pitanja. To opet dovodi do novih znanja i novih pitanja dok se ne riješi polazni problem. To je kurikulum Propitkivanja svijeta, koji zvuči utopijski i nesigurno, ali on zapravo slijedi način na koji znanje nastaje izvan obrazovnog sustava. Ideja u ATD-u jest izgraditi matematičko znanje odgovaranjem na relevantna pitanja čije podrijetlo može biti unutar i izvan matematike tako da se djeluje putem praktičnih i diskurzivnih matematičkih aktivnosti koje su rastuće po svojoj složenosti. U takvom kurikulumu nalaze se sve vrste korelacije, unutarpredmetna i međupredmetna te horizontalna i vertikalna korelacija.
U nastavku je opisana aktivnost propitkivanja u kojoj se pojam funkcionalne ovisnosti izgrađuje rastući po složenosti.
5. Funkcionalna ovisnost
Garcia i suradnici htjeli su osmisliti takvo pitanje koje će dovesti učenike do izučavanja različitih vrsta funkcija [4]. Unutar ATD-a za kurikulum Propitkivanja svijeta ključno je postaviti generativno pitanje iz kojeg proizlaze nova znanja i pitanja. Odgovarajuće pitanje u radu ovih autora glasilo je:
Primjer 4. Želimo unaprijed isplanirati putovanje, izlet na kraju godine. Moramo odlučiti koji će nam plan štednje osigurati dovoljno novaca. Iako ne znamo točan iznos koji će nam trebati, možemo ga procijeniti, možemo odlučiti o rokovima plaćanja, iznosima uplate i drugome. Naravno, ne trebamo odmah odlučiti koliko ćemo novaca prikupiti i na koji način, nego početi raditi na tome, kako bi predvidjeli što ćemo moći napraviti do kraja godine.
Pitanje je otvorenog tipa. Učenici trebaju osmisliti različite planove štednje pri čemu mogu mijenjati iznos početne uplate, broj uplata, iznos jedne uplate, trajanje štednje i promatrati konačne ishode s obzirom na odabrane ulazne podatke. Na taj će način moći izabrati odgovarajući plan kad donesu odluku o izletu i doznaju potreban iznos.
Posao na ovom zadatku ima dvije strane. Učenici provode mnoge i različite praktične i diskurzivne aktivnosti, to su osmišljavanje planova štednje, izračunavanje vrijednosti, tablično i grafičko prikazivanje odabranoga plana štednje te uspoređivanje dobivenih vrijednosti. Potom slijedi postavljanje algebarskog modela plana štednje te uspoređivanje različitih modela koristeći se tim prikazom. S druge strane, izučavaju se funkcije kao vrste zavisnosti između varijabli. Primjerice, plan štednje u kojem se uplati početni iznos $C_0$ i svaki mjesec uplaćuje isti iznos $C$ rezultira linearnom funkcijom s obzirom na broj uplata $x$: $$f(x)=C_0+x\cdot C.$$
Plan štednje u kojem se uplati početni iznos $C_0$ i svaki mjesec uplaćuje iznos za $C$ veći od iznosa u prethodnom mjesecu rezultira kvadratnom funkcijom s obzirom na broj uplata $x$: $$f(x)=C_0+C\cdot\frac{x\cdot(x+1)}{2}.$$
Plan štednje u kojem se uplati početni iznos $C_0$, prvi mjesec se uplati iznos $C$ i svaki sljedeći mjesec uplaćuje iznos $k$ puta veći od iznosa u prethodnom mjesecu rezultira eksponencijalnom funkcijom s obzirom na broj uplata $x$: $$f(x)=C_0+C\cdot\frac{k^x-1}{k-1}.$$
Unutar svakog modela konačni ishodi se, osim po broju uplata, mijenjaju u ovisnosti o početnom iznosu, iznosu uplate, promjenama uplate, što su veličine koje određuju parametre pojedine funkcije. Učenici će uspoređivanjem modela izučavati kako promjena ulaznih podataka u pojedinom planu štednje utječe na konačni ishod, odnosno kako parametri u pojedinoj vrsti funkcije utječu na vrijednosti funkcije, a ne samo kako nezavisna varijabla utječe na vrijednost funkcije.
| Domene: Algebra i funkcije Procesi: Rješavanje problema i matematičko modeliranje, Prikazivanje i komunikacija Aktivnosti: Osmišljavanje različitih planova štednje kao različitih vrsta zavisnosti između varijabli jer se mijenja broj i iznos uplata kako bismo se pripremili za isplatu kad se odredi potreban iznos. |
Literatura
- Chevallard, Y., Introducing the Anthropological Theory of the Didactic: An attempt at a principled approach, Hiroshima Journal of Mathematics Education, 12, 71–114, 2019.
- Dakić, B. i Elezović, N., Matematika 4, udžbenik i zbirka zadataka za 4. razred gimnazije, 2.dio, Element, 2007.
- Dika, A. i Skočić, N., Kutija maksimalnog volumena, Matematika i škola, 53, 125-130, 2010.
- García, F. J., Pérez, J. G., Higueras, L. R. i Bosch, M., Mathematical modelling as a tool for the connection of school mathematics, ZDM, 38(3), 226–246., 2006.
- Keček, D., Poldrugač, A. i Vuković, P., Poopćenja Pitagorinog poučka, Tehnički glasnik, 7(2), 103–107, 2013.
- Kos, S., Razvijanje logičkog mišljenja, argumentiranja i zaključivanja u početnoj nastavi matematike, diplomski rad, https://urn.nsk.hr/urn:nbn:hr:141:428046, 2015.
- Kurikulumi nastavnih predmeta Matematika za osnovne škole i gimnazije i Matematika za srednje strukovne škole na razini 4.2., Ministarstvo znanosti i obrazovanja, 2019., https://skolazazivot.hr/wp-content/uploads/2020/07/MAT_kurikulum_1_71.pdf
- Lerman, S. (Ur.)., Encyclopedia of Mathematics Education, Springer Netherlands, 2014.
